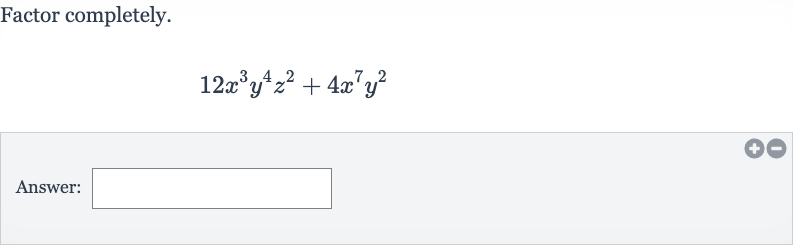Factor completely. 12x^(3)y^(4)z^(2)+4x^(7)y^(2) Answer:

Question

Factor completely.  12x^(3)y^(4)z^(2)+4x^(7)y^(2) Answer:

Bytelearn · Accepted Answer

Identify GCF: Identify the greatest common factor (GCF) of the terms 12x^(3)y^(4)z^(2) and 4x^(7)y^(2). The GCF of the numerical coefficients (12 and 4) is 4. The GCF of the x terms (x^(3) and x^(7)) is x^(3), since we take the lowest power. The GCF of the y terms (y^(4) and y^(2)) is y^(2), since we take the lowest power. There is no z term in the second term, so z^(2) is not part of the GCF. The GCF is therefore 4x^(3)y^(2).Factor out GCF: Factor out the GCF from the original expression. 4x^(3)y^(2) is factored out, leaving us with the expression inside the parentheses. 12x^(3)y^(4)z^(2) divided by 4x^(3)y^(2) gives us 3y^(2)z^(2). 4x^(7)y^(2) divided by 4x^(3)y^(2) gives us x^(4). The factored expression is 4x^(3)y^(2)(3y^(2)z^(2) + x^(4)).Check factored expression: Check the factored expression by distributing the GCF back into the parentheses to ensure it gives us the original expression. 4x^(3)y^(2)(3y^(2)z^(2)) = 12x^(3)y^(4)z^(2). 4x^(3)y^(2)(x^(4)) = 4x^(7)y^(2). The original expression is recovered, confirming the factoring is correct.

Factor completely. $\newline$ $12 x^{3} y^{4} z^{2}+4 x^{7} y^{2}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely.\newline12x3y4z2+4x7y2 12 x^{3} y^{4} z^{2}+4 x^{7} y^{2} 12x3y4z2+4x7y2\newlineAnswer:

Factor completely. $\newline$ $12 x^{3} y^{4} z^{2}+4 x^{7} y^{2}$ $\newline$ Answer: