AI tutor
Full solution
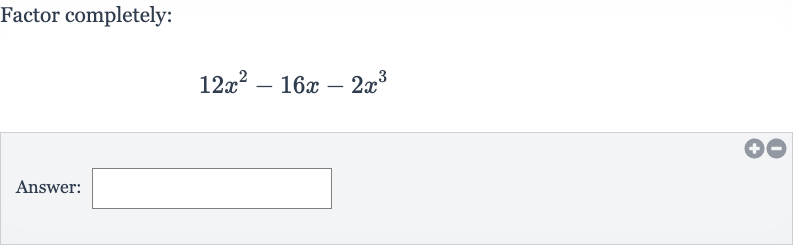
Q. Factor completely:Answer:
- Rearrange terms in descending order: First, we should rearrange the terms in descending order of the powers of . can be rewritten as .
- Factor out greatest common factor: Next, we can factor out the greatest common factor (GCF) from each term. The GCF of , , and is . Factoring out gives us .
- Factor quadratic expression: Now, we need to factor the quadratic expression . We look for two numbers that multiply to and add up to . These numbers are and . So, we can factor the quadratic as .
- Combine factored terms: Finally, we combine the factored quadratic with the we factored out earlier to get the completely factored form of the polynomial.The final factored form is .