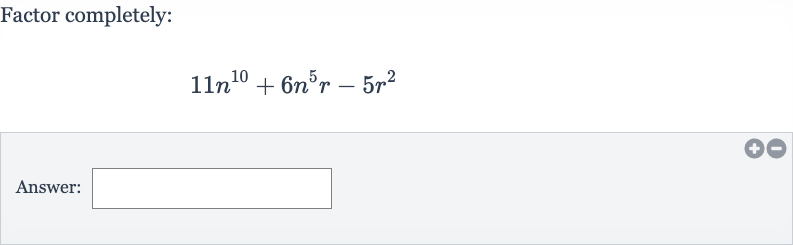
Factor completely: 11n^(10)+6n^(5)r-5r^(2) Answer:

Question

Factor completely:  11n^(10)+6n^(5)r-5r^(2) Answer:

Bytelearn · Accepted Answer

Identify Common Factors: Look for common factors in each term of the polynomial 11n^(10)+6n^(5)r-5r^(2). We notice that there is no common factor for all three terms.Utilize Grouping Method: Since there is no common factor, we look for patterns or special products that might help us factor the polynomial. One pattern that stands out is that the first two terms have a common factor of n^5, and the last two terms do not. This suggests that we might be able to factor by grouping.Factor Out Common Factors: Group the terms with common factors and factor out the greatest common factor from each group. Grouping the first two terms and factoring out n^5 gives us: n^5(11n^5 + 6r) - 5r^2 Now we look at the remaining terms, but there is no common factor between 6r and -5r^2.Search for Binomial Factor: Look for a common binomial factor between the two groups. Since there is no common factor between 6r and -5r^2, we cannot factor by grouping in the usual way. We need to look for another method to factor the polynomial completely.Consider Prime Polynomial: Since the polynomial does not factor by grouping and there are no other apparent patterns, we consider the possibility of it being a prime polynomial, meaning it cannot be factored further over the integers.Conclude Unfactorable: Conclude that the polynomial 11n^(10)+6n^(5)r-5r^(2) is prime and cannot be factored further over the integers.

Factor completely: $\newline$ $11 n^{10}+6 n^{5} r-5 r^{2}$ $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor completely:\newline11n10+6n5r−5r2 11 n^{10}+6 n^{5} r-5 r^{2} 11n10+6n5r−5r2\newlineAnswer:

Factor completely: $\newline$ $11 n^{10}+6 n^{5} r-5 r^{2}$ $\newline$ Answer: