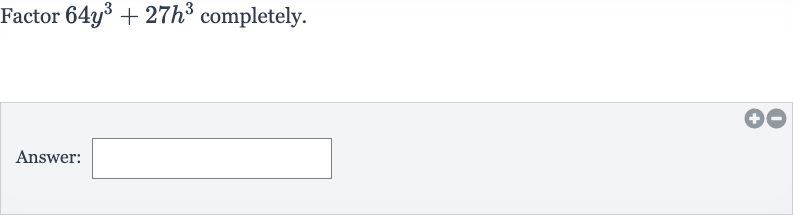
Factor 64y^(3)+27h^(3) completely. Answer:

Question

Factor  64y^(3)+27h^(3) completely. Answer:

Bytelearn · Accepted Answer

Recognize sum of cubes: Recognize the expression as a sum of cubes. The given expression is of the form a^3 + b^3, where a^3 is 64y^3 and b^3 is 27h^3. The sum of cubes can be factored using the formula a^3 + b^3 = (a + b)(a^2 - ab + b^2).Identify values of 'a' and 'b': Identify the values of 'a' and 'b'. In the expression 64y^3 + 27h^3, we can see that a^3 = 64y^3 and b^3 = 27h^3. To find 'a' and 'b', we take the cube root of each term. a = (64y^3)^(1/3) = 4y b = (27h^3)^(1/3) = 3hApply sum of cubes formula: Apply the sum of cubes formula. Using the values of 'a' and 'b' from Step 2, we apply the sum of cubes formula: 64y^3 + 27h^3 = (4y + 3h)((4y)^2 - (4y)(3h) + (3h)^2)Expand and simplify terms: Expand and simplify the terms in the factorization. Now we calculate each term in the formula: (4y)^2 = 16y^2 (4y)(3h) = 12yh (3h)^2 = 9h^2  So the factorization becomes: 64y^3 + 27h^3 = (4y + 3h)(16y^2 - 12yh + 9h^2)Write final factorized form: Write the final factorized form. The completely factorized form of the expression is: 64y^3 + 27h^3 = (4y + 3h)(16y^2 - 12yh + 9h^2)

Factor $64 y^{3}+27 h^{3}$ completely. $\newline$ Answer:

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Factor 64y3+27h3 64 y^{3}+27 h^{3} 64y3+27h3 completely.\newlineAnswer:

Factor $64 y^{3}+27 h^{3}$ completely. $\newline$ Answer: