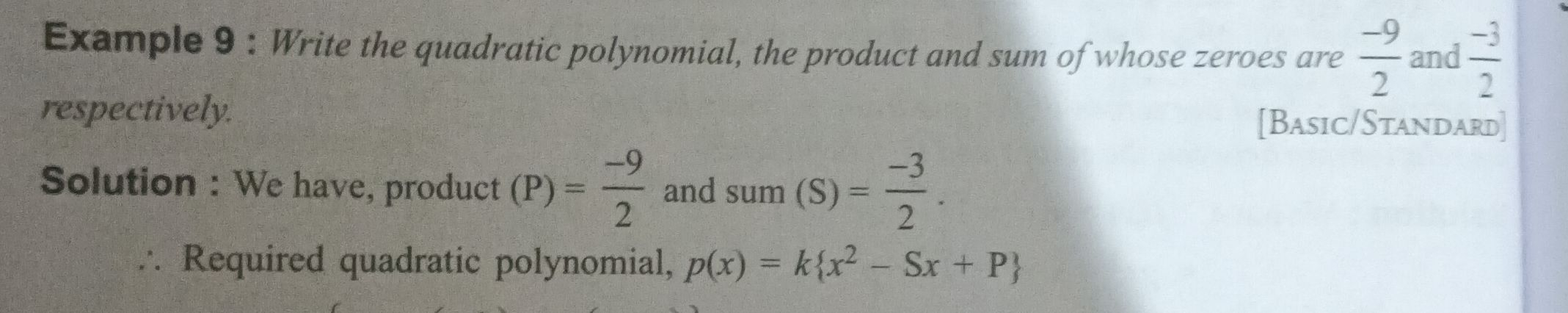Write the quadratic polynomial, the product and sum of whose zeroes are (-9)/(2) and (-3)/(2) respectively.

Question

Write the quadratic polynomial, the product and sum of whose zeroes are (-9)/(2) and  (-3)/(2) respectively.

Bytelearn · Accepted Answer

Identify Product and Zeroes: Identify the product and sum of the zeroes. The product of the zeroes (P) is given as (-9)/(2), and the sum of the zeroes (S) is given as (-3)/(2).Write General Form: Write the general form of a quadratic polynomial. The general form of a quadratic polynomial with zeroes α and β is p(x) = k(x - α)(x - β), where k is a constant.Use Coefficients Relationship: Use the relationship between the coefficients and the zeroes. For a quadratic polynomial p(x) = ax^2 + bx + c, the sum of the zeroes is -b/a and the product of the zeroes is c/a. Here, we have S = -b/a and P = c/a.Substitute Given Values: Substitute the given values of P and S into the relationships. We have S = (-3)/(2) and P = (-9)/(2). Therefore, -b/a = (-3)/(2) and c/a = (-9)/(2).Write Quadratic Polynomial: Write the quadratic polynomial using the values of P and S. Since k is a constant, we can choose k = 1 for simplicity. Thus, the quadratic polynomial is p(x) = x^2 - Sx + P.Substitute Values: Substitute the values of S and P into the polynomial. p(x) = x^2 - ((-3)/(2))x + ((-9)/(2))Simplify Polynomial: Simplify the polynomial. p(x) = x^2 + (3/2)x - (9/2)

Write the quadratic polynomial, the product and sum of whose zeroes are $\frac{-9}{2}$ and $\frac{-3}{2}$ respectively.

Full solution

More problems from Power of a power: integer bases

Related topics

Write the quadratic polynomial, the product and sum of whose zeroes are −92 \frac{-9}{2} 2−9​ and −32 \frac{-3}{2} 2−3​ respectively.

Write the quadratic polynomial, the product and sum of whose zeroes are $\frac{-9}{2}$ and $\frac{-3}{2}$ respectively.