AI tutor
Full solution
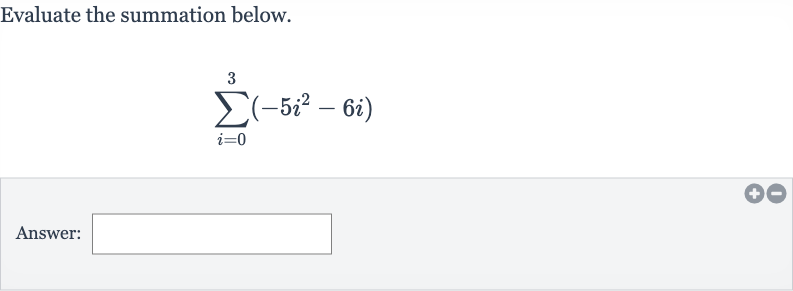
Q. Evaluate the summation below.Answer:
- Understand summation notation: Understand the summation notation and the expression to be summed.The summation notation indicates that we need to sum the expression for each integer value of starting from and ending at .
- Calculate for : Calculate the expression for . For , the expression becomes which simplifies to .
- Calculate for : Calculate the expression for . For , the expression becomes which simplifies to .
- Calculate for : Calculate the expression for . For , the expression becomes which simplifies to .
- Calculate for : Calculate the expression for . For , the expression becomes which simplifies to .
- Sum values: Sum the values from steps to .Sum = Sum = Sum =