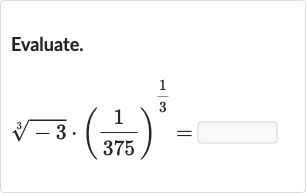AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
Evaluate.
Full solution
Q. Evaluate.
- Evaluate cube root of : First, we need to evaluate the cube root of , which is written as . The cube root of a negative number is negative, so .
- Evaluate cube root of : Next, we evaluate the cube root of , which is written as . To find the cube root of a fraction, we find the cube root of the numerator and the denominator separately.
- Evaluate cube root of : The cube root of is , because raised to any power is . So, .
- Factorize and simplify cube root of : Now, we find the cube root of . We can factor as , and is a perfect cube . So, $(\(375\))^{\(1\)/\(3\)} = (\(3\)\times\(125\))^{\(1\)/\(3\)} = \(3\)^{\(1\)/\(3\)} \times \(125\)^{\(1\)/\(3\)} = \(3\)^{\(1\)/\(3\)} \times \(5\).
- Take reciprocal of cube root of \((1/375)\): Since \(3^{(1/3)}\) is the cube root of \(3\), and we cannot simplify it further without a calculator, we leave it as is. So, \((375)^{(1/3)} = 3^{(1/3)} \times 5\).
- Multiply cube roots of \(-3\) and \((1/375)\): Now, we take the reciprocal of \((375)^{(1/3)}\) because we are dealing with \((1/375)^{(1/3)}\). The reciprocal of \(3^{(1/3)} \times 5\) is \(1 / (3^{(1/3)} \times 5)\).
- Simplify the expression: Multiplying the cube root of \(-3\) by the cube root of \(\frac{1}{375}\), we get: \((-1) \times \left(\frac{1}{3^{\frac{1}{3}} \times 5}\right) = -\frac{1}{3^{\frac{1}{3}} \times 5}\).
- Simplify the expression: Multiplying the cube root of \(-3\) by the cube root of \(\frac{1}{375}\), we get: \((-1) \times \left(\frac{1}{3^{\frac{1}{3}} \times 5}\right) = -\frac{1}{3^{\frac{1}{3}} \times 5}\). Simplify the expression to get the final answer: \(-\frac{1}{3^{\frac{1}{3}} \times 5} = -\frac{1}{5 \times 3^{\frac{1}{3}}}\).
