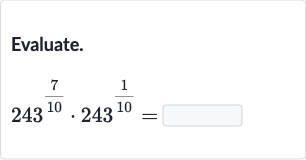AI tutor
Full solution
Q. Evaluate.
- Recognize properties of exponents: Recognize the properties of exponents.When multiplying two expressions with the same base, you can add the exponents.
- Add exponents: Add the exponents.Simplify the fraction to its lowest terms.So,
- Simplify fraction: Evaluate the expression. is raised to the th power , which can be useful when dealing with fractional exponents.Use the property of exponents .
- Evaluate expression: Simplify the exponent.So,
- Simplify exponent: Calculate the value of .
More problems from Solve multi-step linear equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help