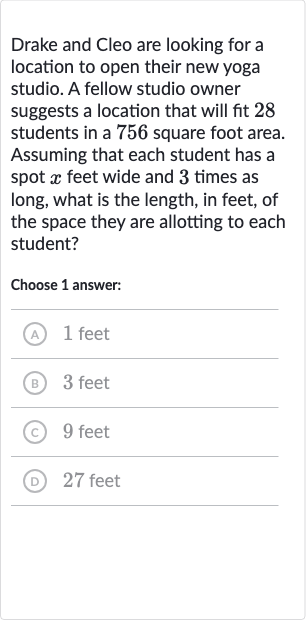
Drake and Cleo are looking for a location to open their new yoga studio. A fellow studio owner suggests a location that will fit 28 students in a 756 square foot area. Assuming that each student has a spot x feet wide and 3 times as long, what is the length, in feet, of the space they are allotting to each student? Choose 1 answer: (A) 1 feet (B) 3 feet (C) 9 feet (D) 27 feet

Question

Drake and Cleo are looking for a location to open their new yoga studio. A fellow studio owner suggests a location that will fit 28 students in a 756 square foot area. Assuming that each student has a spot  x feet wide and 3 times as long, what is the length, in feet, of the space they are allotting to each student? Choose 1 answer: (A) 1 feet (B) 3 feet (C) 9 feet (D) 27 feet

Bytelearn · Accepted Answer

Determine Area Allocation: First, we need to determine the area allocated to each student. Since the total area is 756 square feet and there are 28 students, we divide the total area by the number of students. Calculation: 756 square feet / 28 students = 27 square feet per student.Calculate Spot Area: Next, we know that each student's spot is x feet wide and 3 times as long. This means the area of each spot is x * (3x), which should equal the area per student we found in the previous step. Setting up the equation: x * (3x) = 27.Solve for Width: Now we need to solve for x. We have a quadratic equation: 3x^2 = 27. Divide both sides by 3 to simplify the equation: x^2 = 9.Find Length: To find the value of x, we take the square root of both sides of the equation: √(x^2) = √(9). This gives us x = 3 or x = -3. Since we are looking for a length, we only consider the positive value.Final Length Calculation: Finally, since the length of each spot is 3 times the width, we multiply the width (x) by 3 to find the length. Calculation: Length = 3 * x = 3 * 3 = 9 feet.

Full solution

More problems from Solve linear equations with variables on both sides: word problems

Related topics