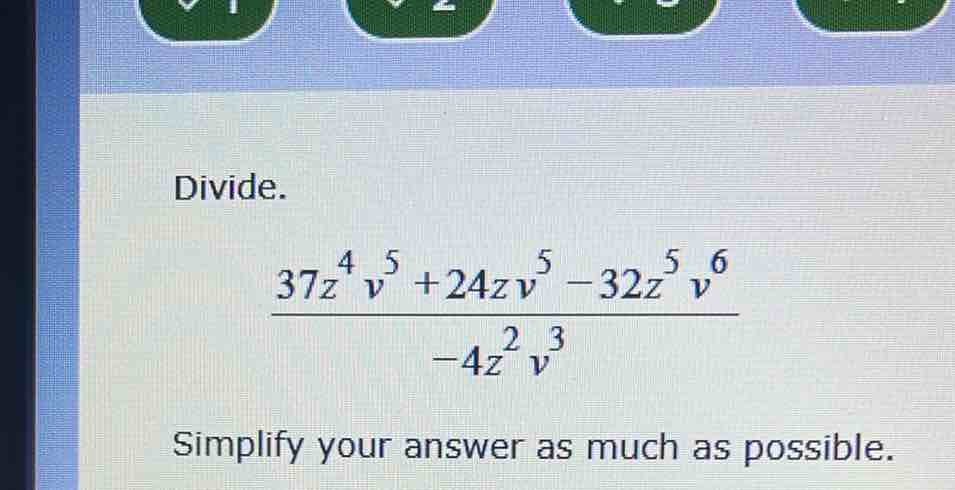Divide. (37z^(4)v^(5)+24 zv^(5)-32z^(5)v^(6))/(-4z^(2)v^(3)) Simplify your answer as much as possible.

Question

Divide.  (37z^(4)v^(5)+24 zv^(5)-32z^(5)v^(6))/(-4z^(2)v^(3)) Simplify your answer as much as possible.

Bytelearn · Accepted Answer

Divide by Negative Exponent: To simplify the given expression, we will divide each term in the numerator by the term in the denominator. The expression is (37z^(4)v^(5)+24 zv^(5)-32z^(5)v^(6))/(-4z^(2)v^(3)).Simplify First Term: First, divide the term 37z^(4)v^(5) by -4z^(2)v^(3). We subtract the exponents of like bases in the numerator and the denominator and change the sign because of the negative divisor. 37z^(4)v^(5) / -4z^(2)v^(3) = -37/4 * z^(4-2) * v^(5-3) = -37/4 * z^2 * v^2.Simplify Second Term: Next, divide the term 24zv^(5) by -4z^(2)v^(3). Again, we subtract the exponents of like bases and change the sign because of the negative divisor. 24zv^(5) / -4z^(2)v^(3) = -24/4 * z^(1-2) * v^(5-3) = -6 * z^(-1) * v^2 = -6/z * v^2.Simplify Third Term: Finally, divide the term -32z^(5)v^(6) by -4z^(2)v^(3). We subtract the exponents of like bases and the negatives cancel each other out. -32z^(5)v^(6) / -4z^(2)v^(3) = 32/4 * z^(5-2) * v^(6-3) = 8 * z^3 * v^3.Combine Simplified Terms: Combine all the simplified terms to get the final simplified expression. (-37/4 * z^2 * v^2) + (-6/z * v^2) + (8 * z^3 * v^3).

Divide. $\newline$ $\frac{37 z^{4} v^{5}+24 z v^{5}-32 z^{5} v^{6}}{-4 z^{2} v^{3}}$ $\newline$ Simplify your answer as much as possible.

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Divide.\newline37z4v5+24zv5−32z5v6−4z2v3 \frac{37 z^{4} v^{5}+24 z v^{5}-32 z^{5} v^{6}}{-4 z^{2} v^{3}} −4z2v337z4v5+24zv5−32z5v6​\newlineSimplify your answer as much as possible.

Divide. $\newline$ $\frac{37 z^{4} v^{5}+24 z v^{5}-32 z^{5} v^{6}}{-4 z^{2} v^{3}}$ $\newline$ Simplify your answer as much as possible.