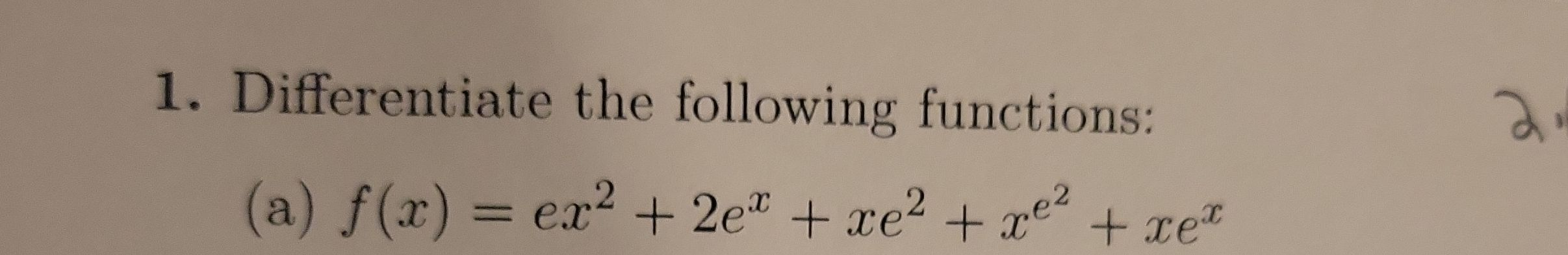Differentiate the following functions: (a) f(x)=ex^(2)+2e^(x)+xe^(2)+x^(e^(2))+xe^(x)

Question

Differentiate the following functions: (a)  f(x)=ex^(2)+2e^(x)+xe^(2)+x^(e^(2))+xe^(x)

Bytelearn · Accepted Answer

Apply Sum Rule: To differentiate the function f(x) = e^(x^2) + 2e^x + xe^2 + x^(e^2) + xe^x, we will apply the sum rule of differentiation, which allows us to differentiate each term separately.Differentiate e^(x^2): Differentiate the first term e^(x^2) with respect to x using the chain rule. The derivative of e^u with respect to x is e^u * (du/dx), where u = x^2 in this case. (d/dx)(e^(x^2)) = e^(x^2) * (d/dx)(x^2) = e^(x^2) * 2xDifferentiate 2e^x: Differentiate the second term 2e^x with respect to x. The derivative of a constant times a function is the constant times the derivative of the function. (d/dx)(2e^x) = 2 * (d/dx)(e^x) = 2 * e^xDifferentiate xe^2: Differentiate the third term xe^2 with respect to x. Since e^2 is a constant, the derivative of a constant times x is just the constant. (d/dx)(xe^2) = e^2Differentiate x^(e^2): Differentiate the fourth term x^(e^2) with respect to x. The derivative of x to a constant power is the constant power times x raised to the power minus one. (d/dx)(x^(e^2)) = e^2 * x^(e^2 - 1)Differentiate xe^x: Differentiate the fifth term xe^x with respect to x using the product rule. The product rule states that (d/dx)(uv) = u'(v) + u(v'), where u = x and v = e^x. (d/dx)(xe^x) = (d/dx)(x) * e^x + x * (d/dx)(e^x) = 1 * e^x + x * e^x = e^x + xe^xCombine Derivatives: Combine the derivatives of all terms to get the derivative of the entire function f(x). f'(x) = (d/dx)(e^(x^2)) + (d/dx)(2e^x) + (d/dx)(xe^2) + (d/dx)(x^(e^2)) + (d/dx)(xe^x) f'(x) = e^(x^2) * 2x + 2 * e^x + e^2 + e^2 * x^(e^2 - 1) + e^x + xe^xSimplify Expression: Simplify the expression for the derivative. f'(x) = 2xe^(x^2) + 2e^x + e^2 + e^2 * x^(e^2 - 1) + e^x + xe^x

$1$ . Differentiate the following functions: $\newline$ (a) $f(x)=e x^{2}+2 e^{x}+x e^{2}+x^{e^{2}}+x e^{x}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

111. Differentiate the following functions:\newline(a) f(x)=ex2+2ex+xe2+xe2+xex f(x)=e x^{2}+2 e^{x}+x e^{2}+x^{e^{2}}+x e^{x} f(x)=ex2+2ex+xe2+xe2+xex

$1$ . Differentiate the following functions: $\newline$ (a) $f(x)=e x^{2}+2 e^{x}+x e^{2}+x^{e^{2}}+x e^{x}$