Full solution
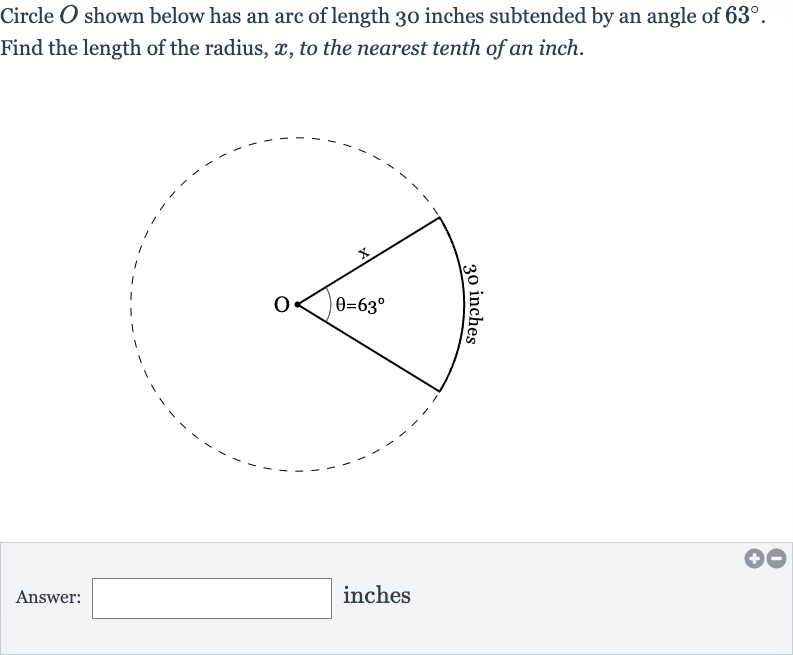
Q. Circle shown below has an arc of length inches subtended by an angle of .Find the length of the radius, , to the nearest tenth of an inch.Answer: inches
- Convert degrees to radians: To find the radius of the circle, we can use the formula for the length of an arc, which is , where is the arc length, is the radius, and is the central angle in radians. Since we have the angle in degrees, we need to convert it to radians first.
- Calculate angle in radians: To convert degrees to radians, we use the conversion factor . So, degrees is radians.
- Use arc length formula: Now, let's calculate the angle in radians: radians (using ).
- Calculate radius: With the angle in radians, we can now use the arc length formula to find the radius. We have inches and radians. We need to solve for : .
- Round to nearest tenth: Plugging in the values, we get . Let's calculate this value.
- Round to nearest tenth: Plugging in the values, we get . Let's calculate this value.The calculation gives us inches. However, we need to round this to the nearest tenth of an inch.
- Round to nearest tenth: Plugging in the values, we get . Let's calculate this value.The calculation gives us inches. However, we need to round this to the nearest tenth of an inch.Rounding inches to the nearest tenth gives us inches, as it is already at the tenth place.
More problems from Circles: word problems
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help