Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Circle
O shown below has a radius of 8 inches. To the nearest tenth of an inch, determine the length of the arc,
x, subtended by an angle of
136^(@).
Answer: inches

Circle $O$ shown below has a radius of $8$ inches. To the nearest tenth of an inch, determine the length of the arc, $x$ , subtended by an angle of $136^{\circ}$ . $\newline$ Answer: $\square$ inches

View step-by-step help

View step-by-step help

Circles: word problems

Full solution

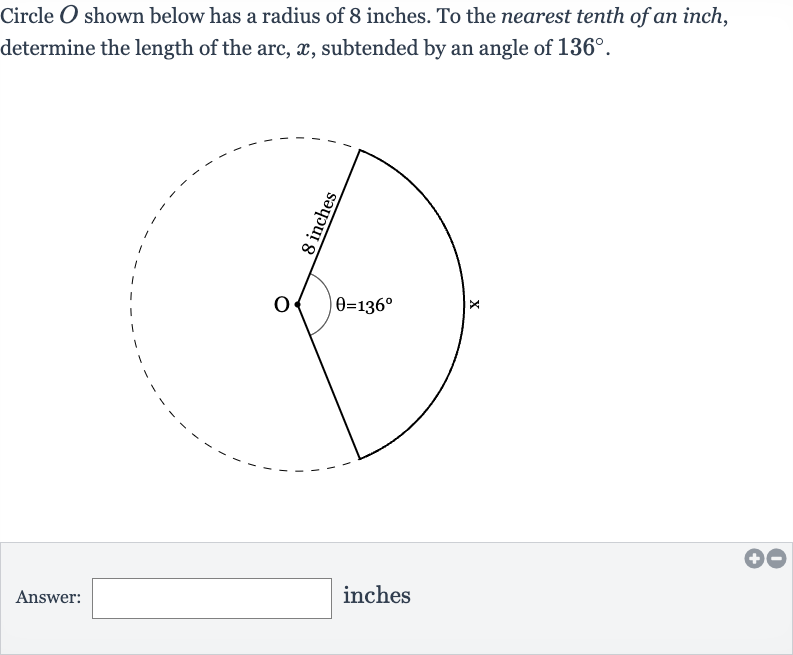
Q. Circle

O

shown below has a radius of

8

inches. To the nearest tenth of an inch, determine the length of the arc,

x

, subtended by an angle of

136^{\circ}

.

\newline

Answer:

\square

inches

Understand Relationship: Understand the relationship between the angle subtended by an arc, the radius of the circle, and the length of the arc. $\newline$ The formula to find the length of an arc $s$ is $s = r\theta$ , where $r$ is the radius and $\theta$ is the angle in radians. $\newline$ To convert degrees to radians, we use the conversion factor $\pi$ radians $= 180$ degrees.
Convert to Radians: Convert the angle from degrees to radians. $\newline$ We have an angle of $136$ degrees. To convert it to radians, we multiply by $\pi/180$ . $\newline$ $\theta$ in radians = $136 \times (\pi/180)$ .
Calculate Angle: Calculate the angle in radians. $\newline$ $\theta$ in radians = $136 \times (\pi/180) = \frac{136\pi}{180}$ . $\newline$ We can simplify this fraction by dividing both the numerator and the denominator by $4$ . $\newline$ $\theta$ in radians = $(136/4)\pi/(180/4) = \frac{34\pi}{45}$ .
Use Arc Length Formula: Use the formula for the arc length with the radius and the angle in radians. $\newline$ We know the radius $r$ is $8$ inches and $\theta$ in radians is $\frac{34\pi}{45}$ . $\newline$ Arc length $s$ = $r\theta = 8 \times \left(\frac{34\pi}{45}\right)$ .
Calculate Arc Length: Calculate the arc length. $\newline$ Arc length $s$ = $8 \times (34\pi/45)$ = $(8 \times 34\pi)/45$ = $272\pi/45$ .
Evaluate Using Approximation: Evaluate the arc length using the approximation for $\pi$ ( $\pi \approx 3.14$ ). $\newline$ Arc length (s) $\approx (272 \times 3.14)/45$ .
Perform Multiplication and Division: Perform the multiplication and division to find the arc length. Arc length $s$ $\approx$ $\frac{854.88}{45}$ $\approx$ $18.9973333$ inches.
Round to Nearest Tenth: Round the arc length to the nearest tenth of an inch. $\newline$ Arc length $s$ $\approx 19.0$ inches.

More problems from Circles: word problems

Question

Skyler climbs a watchtower to guard against forest fires.

\newline

R(h)=\sqrt{13h}

gives the distance, in kilometers, that Skyler can see when their eyes are

h

meters above the ground.

\newline

A(d)=\pi d^{2}

gives the area, in square kilometers, that Skyler can guard when they can see a distance of

d

\newline

Which expression models the area Skyler can guard when their eyes are

h

meters above the ground?

\newline

1

\newline

13\pi h

\newline

13\pi h^{2}

\newline

\sqrt{13\pi h^{2}}

\newline

169\pi h^{2}

Posted 2 months ago

Question

After the outbreak of a mysterious disease, the average wait time at a hospital increased by

70\%

. Before the outbreak, the average wait time at the hospital was

m

\newline

Which of the following expressions could represent the average wait time at the hospital after the outbreak?

\newline

2

\newline

0.7m

\newline

\frac{170}{100}m

\newline

m+70

\newline

m+0.7

\newline

1.7m

Posted 1 month ago

Question

The radius of a semicircle is

3

yards. What is the semicircle's area?

\newline

\pi \approx 3.14

and round your answer to the nearest hundredth.

\newline

Posted 2 months ago

Question

\newline

A man has bent a circular wire of radius

49\text{cm}

to form a square. Find the sides of a square.

\newline

A)100\text{cm}

\newline

B)50\text{cm}

\newline

C)98\text{cm}

Posted 2 months ago

Question

A quarter is worth

\$0.25

and a half dollar is worth

\$0.50

\newline

a. A quarter has a diameter of

\frac{15}{16}

inch and a height of

\frac{1}{16}

inch. Find the surface area of a quarter. Round your answer to the nearest hundredth.

\newline

b. A half dollar has a diameter of

\frac{9}{8}

inches and a height of

\frac{3}{32}

inch. Find the surface area of a half dollar. Round your answer to the nearest hundredth.

Posted 2 months ago

Question

The hypotenuse of a right triangle measures

17 \mathrm{~cm}

and one of its legs measures

8 \mathrm{~cm}

. Find the measure of the other leg. If necessary, round to the nearest tenth.

\newline

\square

\mathrm{cm}

Posted 3 months ago

Question

One of the legs of a right triangle measures

15 \mathrm{~cm}

and its hypotenuse measures

17 \mathrm{~cm}

. Find the measure of the other leg. If necessary, round to the nearest tenth.

\newline

\square

\mathrm{cm}

Posted 3 months ago

Question

One of the legs of a right triangle measures

8 \mathrm{~cm}

and the other leg measures

15 \mathrm{~cm}

. Find the measure of the hypotenuse. If necessary, round to the nearest tenth.

\newline

\square

\mathrm{cm}

Posted 3 months ago

Question

Find the volume of a right circular cone that has a height of

7.4 \mathrm{~cm}

and a base with a radius of

8.1 \mathrm{~cm}

. Round your answer to the nearest tenth of a cubic centimeter.

\newline

\mathrm{cm}^{3}

Posted 3 months ago

Question

Find the volume of a right circular cone that has a height of

13.3 \mathrm{ft}

and a base with a diameter of

9.4 \mathrm{ft}

. Round your answer to the nearest tenth of a cubic foot.

\newline

\mathrm{ft}^{3}

Posted 3 months ago