Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Circle
O shown below has a radius of 11 inches. To the nearest tenth of an inch, determine the length of the arc,
x, subtended by an angle of
145^(@).
Answer: inches

Circle $O$ shown below has a radius of $11$ inches. To the nearest tenth of an inch, determine the length of the arc, $x$ , subtended by an angle of $145^{\circ}$ . $\newline$ Answer: $\square$ inches

View step-by-step help

View step-by-step help

Circles: word problems

Full solution

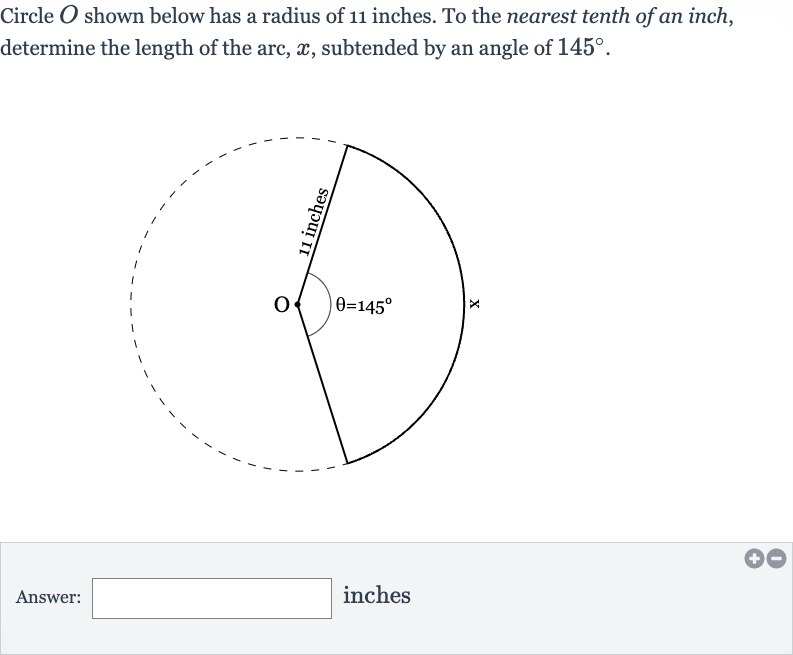
Q. Circle

O

shown below has a radius of

11

inches. To the nearest tenth of an inch, determine the length of the arc,

x

, subtended by an angle of

145^{\circ}

.

\newline

Answer:

\square

inches

Identify formula: Identify the formula to calculate the length of an arc. $\newline$ The length of an arc $L$ in a circle is given by the formula $L = (\theta/360) \times 2\pi r$ , where $\theta$ is the central angle in degrees and $r$ is the radius of the circle.
Plug values: Plug in the given values into the formula. $\newline$ Here, $\theta = 145$ degrees and $r = 11$ inches. Using the approximation $\pi \approx 3.14$ , we can calculate the length of the arc. $\newline$ $L = (\frac{145}{360}) \times 2 \times 3.14 \times 11$
Calculate arc length: Calculate the length of the arc. $\newline$ First, calculate the fraction of the circle that the arc covers by dividing the angle by $360$ degrees. $\newline$ $\frac{145}{360} \approx 0.4028$ (rounded to four decimal places for precision in intermediate steps) $\newline$ Now, multiply this fraction by the circumference of the entire circle $(2 \cdot \pi \cdot r)$ . $\newline$ $L \approx 0.4028 \cdot 2 \cdot 3.14 \cdot 11$
Perform multiplication: Perform the multiplication to find the length of the arc. $\newline$ $L \approx 0.4028 \times 2 \times 3.14 \times 11$ $\newline$ $L \approx 0.4028 \times 69.08$ (since $2 \times 3.14 \times 11 = 69.08$ ) $\newline$ $L \approx 27.8264$ inches
Round result: Round the result to the nearest tenth of an inch as the problem asks. $\newline$ $L \approx 27.8$ inches (rounded to the nearest tenth)

More problems from Circles: word problems

Question

Skyler climbs a watchtower to guard against forest fires.

\newline

R(h)=\sqrt{13h}

gives the distance, in kilometers, that Skyler can see when their eyes are

h

meters above the ground.

\newline

A(d)=\pi d^{2}

gives the area, in square kilometers, that Skyler can guard when they can see a distance of

d

\newline

Which expression models the area Skyler can guard when their eyes are

h

meters above the ground?

\newline

1

\newline

13\pi h

\newline

13\pi h^{2}

\newline

\sqrt{13\pi h^{2}}

\newline

169\pi h^{2}

Posted 2 months ago

Question

After the outbreak of a mysterious disease, the average wait time at a hospital increased by

70\%

. Before the outbreak, the average wait time at the hospital was

m

\newline

Which of the following expressions could represent the average wait time at the hospital after the outbreak?

\newline

2

\newline

0.7m

\newline

\frac{170}{100}m

\newline

m+70

\newline

m+0.7

\newline

1.7m

Posted 1 month ago

Question

The radius of a semicircle is

3

yards. What is the semicircle's area?

\newline

\pi \approx 3.14

and round your answer to the nearest hundredth.

\newline

Posted 2 months ago

Question

\newline

A man has bent a circular wire of radius

49\text{cm}

to form a square. Find the sides of a square.

\newline

A)100\text{cm}

\newline

B)50\text{cm}

\newline

C)98\text{cm}

Posted 2 months ago

Question

A quarter is worth

\$0.25

and a half dollar is worth

\$0.50

\newline

a. A quarter has a diameter of

\frac{15}{16}

inch and a height of

\frac{1}{16}

inch. Find the surface area of a quarter. Round your answer to the nearest hundredth.

\newline

b. A half dollar has a diameter of

\frac{9}{8}

inches and a height of

\frac{3}{32}

inch. Find the surface area of a half dollar. Round your answer to the nearest hundredth.

Posted 2 months ago

Question

The hypotenuse of a right triangle measures

17 \mathrm{~cm}

and one of its legs measures

8 \mathrm{~cm}

. Find the measure of the other leg. If necessary, round to the nearest tenth.

\newline

\square

\mathrm{cm}

Posted 2 months ago

Question

One of the legs of a right triangle measures

15 \mathrm{~cm}

and its hypotenuse measures

17 \mathrm{~cm}

. Find the measure of the other leg. If necessary, round to the nearest tenth.

\newline

\square

\mathrm{cm}

Posted 2 months ago

Question

One of the legs of a right triangle measures

8 \mathrm{~cm}

and the other leg measures

15 \mathrm{~cm}

. Find the measure of the hypotenuse. If necessary, round to the nearest tenth.

\newline

\square

\mathrm{cm}

Posted 2 months ago

Question

Find the volume of a right circular cone that has a height of

7.4 \mathrm{~cm}

and a base with a radius of

8.1 \mathrm{~cm}

. Round your answer to the nearest tenth of a cubic centimeter.

\newline

\mathrm{cm}^{3}

Posted 2 months ago

Question

Find the volume of a right circular cone that has a height of

13.3 \mathrm{ft}

and a base with a diameter of

9.4 \mathrm{ft}

. Round your answer to the nearest tenth of a cubic foot.

\newline

\mathrm{ft}^{3}

Posted 2 months ago