Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

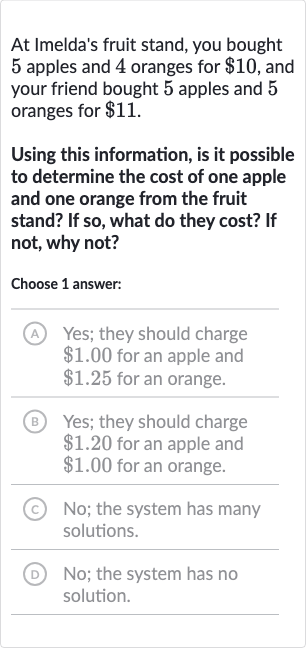
At Imelda's fruit stand, you bought 5 apples and 4 oranges for
$10, and your friend bought 5 apples and 5 oranges for
$11.
Using this information, is it possible to determine the cost of one apple and one orange from the fruit stand? If so, what do they cost? If not, why not?
Choose 1 answer:
(A) Yes; they should charge
$1.00 for an apple and
$1.25 for an orange.
(B) Yes; they should charge
$1.20 for an apple and
$1.00 for an orange.
(C) No; the system has many solutions.
(D) No; the system has no solution.

At Imelda's fruit stand, you bought $5$ apples and $4$ oranges for $\$10$ , and your friend bought $5$ apples and $5$ oranges for $\$11$ . Using this information, is it possible to determine the cost of one apple and one orange from the fruit stand? If so, what do they cost? If not, why not? $\newline$ Choose $1$ answer: $\newline$ (A) Yes; they should charge $\$1.00$ for an apple and $\$1.25$ for an orange. $\newline$ (B) Yes; they should charge $\$1.20$ for an apple and $\$1.00$ for an orange. $\newline$ (C) No; the system has many solutions. $\newline$ (D) No; the system has no solution.

View step-by-step help

View step-by-step help

Add and subtract integers: word problems

Full solution

Q. At Imelda's fruit stand, you bought

5

apples and

4

oranges for

\$10

, and your friend bought

5

apples and

5

oranges for

\$11

. Using this information, is it possible to determine the cost of one apple and one orange from the fruit stand? If so, what do they cost? If not, why not?

\newline

Choose

1

answer:

\newline

(A) Yes; they should charge

\$1.00

for an apple and

\$1.25

for an orange.

\newline

(B) Yes; they should charge

\$1.20

for an apple and

\$1.00

for an orange.

\newline

(C) No; the system has many solutions.

\newline

(D) No; the system has no solution.

Equations Setup: Let's denote the cost of one apple as $A$ and the cost of one orange as $O$ . We can set up two equations based on the information given: $\newline$ For your purchase: $5A + 4O = (\$)10$ $\newline$ For your friend's purchase: $5A + 5O = (\$)11$
Elimination Method: We can subtract the first equation from the second to eliminate the apples and solve for the cost of one orange: $\newline$ $(5A + 5O) - (5A + 4O) = (\$11) - (\$10)$ $\newline$ This simplifies to $O = \$1$
Substitution: Now that we know the cost of one orange is $\$1$ , we can substitute this value back into the first equation to find the cost of one apple: $\newline$ $5A + 4(1) = \$10$ $\newline$ $5A + \$4 = \$10$ $\newline$ $5A = \$10 - \$4$ $\newline$ $5A = \$6$ $\newline$ $A = \$6 / 5$ $\newline$ $A = \$1.20$
Final Cost Calculation: We have found the cost of one apple to be \$\(1\).\(20\) and the cost of one orange to be \$\(1\).\(00\). This matches one of the answer choices provided.

More problems from Add and subtract integers: word problems

Question

g

can be thought of as a scaled version of

f(x)=|x|

\newline

What is the equation for

g(x)

\newline

1

\newline

g(x)=-\frac{4}{3}|x|

\newline

g(x)=\frac{4}{3}|x|

\newline

g(x)=-\frac{3}{4}|x|

\newline

g(x)=\frac{3}{4}|x|

Posted 8 months ago

Question

y=|x|

is reflected across the

x

-axis and then scaled vertically by a factor of

\frac{5}{3}

\newline

What is the equation of the new graph?

\newline

1

\newline

y=-\frac{5}{3}|x|

\newline

y=\frac{3}{5}|x|

\newline

y=-|x-5|+3

\newline

y=|x-3|+5

Posted 10 months ago

Question

\$ 200

with which to purchase hats and t-shirts that are to be sold at his class' next fundraiser. Each hat costs the same amount of money, and each t-shirt costs the same amount of money. If Aiden spends all his money entirely on hats, he will get

40

hats. If Aiden purchases only

t

-shirts, he will get

80

\mathrm{t}

-shirts. Which of the following best models the relationship between the number of hats,

h

, and the number of

\mathrm{t}

t

, that Aiden could purchase with this money?

\newline

1

\newline

40 h+80 t=400

\newline

80 h+40 t=200

\newline

5 h+2.5 t=200

\newline

2.5 h+5 t=200

Posted 10 months ago

Question

We want to find the intersection points of the graphs given by the following system of equations:

\newline

\left\{\begin{array}{l} x-y=-4 \\ y=5(x+1)^{2}-3 \end{array}\right.

\newline

One of the intersection points is

(-2,2)

\newline

Find the other intersection point. Your answer must be exact.

Posted 10 months ago

Question

\mathbf{2 2}

dollars. Colleen has

x

dollars. Which of the following represents the total amount of money Derrick and Colleen have, in dollars?

\newline

1

\newline

x-22

\newline

x+22

\newline

22 x

\newline

22 x+22

Posted 10 months ago

Question

Wilber wants to make the pond in his backyard bigger. It is currently a cone with a radius of

30

meters and a depth of

15

meters. He wants to increase the radius to

40

meters and the depth to

20

meters. How much more water will the pond hold, in thousands of cubic meters?

\newline

(Round to the nearest thousand cubic meters.)

Posted 4 months ago

Question

Abby is buying a rectangular widescreen TV that she will hang on the wall between two windows such that the longer side of the TV is horizontal. The windows are

36

inches apart horizontally, and a widescreen TV is approximately twice as wide as it is tall. Which of the following could be the diagonal length of a widescreen TV that fits between the windows?

\newline

1

\newline

32

\newline

42

\newline

55

\newline

60

Posted 7 months ago

Question

Ari thinks the perfect milkshake has

5

scoops of ice cream for every

3

spoonfuls of caramel. Freeze Zone makes batches of milkshakes with

10

scoops of ice cream and

7

spoonfuls of caramel.

\newline

What will Ari think about the amount of caramel in Freeze Zone's milkshakes?

\newline

1

\newline

(A) Freeze Zone's milkshakes have too much caramel.

\newline

(B) Freeze Zone's milkshakes have too little caramel.

\newline

(C) Freeze Zone's milkshakes are just right.

Posted 8 months ago

Question

Nayeli lights a

4 \mathrm{~m}^{2}

12

candles. Citlali lights a

10 \mathrm{~m}^{2}

30

of the same type of candles.

\newline

Whose space is lit brighter?

\newline

1

\newline

(A) Nayeli's area

\newline

(B) Citlali's area

\newline

(C) The spaces are equally bright.

Posted 5 months ago

Question

Lashawn makes scrambled eggs with

3

spoonfuls of salsa for every

2

eggs. Gilberta adds

7

spoonfuls of salsa for every

5

\newline

Whose scrambled eggs have a stronger salsa taste?

\newline

1

\newline

(A) Lashawn's eggs

\newline

(B) Gilberta's eggs

\newline

(C) The dishes of scrambled eggs have equal salsa tastes.

Posted 8 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant