Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

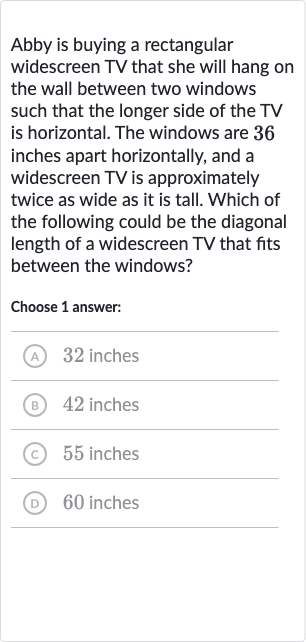
Abby is buying a rectangular widescreen TV that she will hang on the wall between two windows such that the longer side of the TV is horizontal. The windows are 36 inches apart horizontally, and a widescreen TV is approximately twice as wide as it is tall. Which of the following could be the diagonal length of a widescreen TV that fits between the windows? Choose 1 answer: (A) 32 inches (B) 42 inches (C) 55 inches (D) 60 inches

Abby is buying a rectangular widescreen TV that she will hang on the wall between two windows such that the longer side of the TV is horizontal. The windows are 3636 inches apart horizontally, and a widescreen TV is approximately twice as wide as it is tall. Which of the following could be the diagonal length of a widescreen TV that fits between the windows?\newlineChoose 11 answer:\newline(A) 3232 inches\newline(B) 4242 inches\newline(C) 5555 inches\newline(D) 6060 inches

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 7right chevron icon
Quantities that combine to zero: word problemsright chevron icon

Full solution

Q. Abby is buying a rectangular widescreen TV that she will hang on the wall between two windows such that the longer side of the TV is horizontal. The windows are 3636 inches apart horizontally, and a widescreen TV is approximately twice as wide as it is tall. Which of the following could be the diagonal length of a widescreen TV that fits between the windows?\newlineChoose 11 answer:\newline(A) 3232 inches\newline(B) 4242 inches\newline(C) 5555 inches\newline(D) 6060 inches
  1. Understand Problem: Understand the problem and the given information.\newlineThe space between the windows is 3636 inches, and the TV's aspect ratio is approximately 2:12:1, meaning the width is twice the height. We need to find a TV size that fits within this space, considering the diagonal length.
  2. Denote TV Dimensions: Let's denote the height of the TV as hh and the width as ww. According to the aspect ratio, w=2hw = 2h. The diagonal dd can be found using the Pythagorean theorem, where d2=h2+w2d^2 = h^2 + w^2.
  3. Substitute in Pythagorean Theorem: Substitute the width in terms of height into the Pythagorean theorem.\newlined2=h2+(2h)2d^2 = h^2 + (2h)^2\newlined2=h2+4h2d^2 = h^2 + 4h^2\newlined2=5h2d^2 = 5h^2
  4. Set Width Constraint: Since the width of the TV must be less than or equal to 3636 inches to fit between the windows, we set w≤36w \leq 36 inches. Therefore, 2h≤362h \leq 36 inches, which implies h≤18h \leq 18 inches.
  5. Calculate Maximum Diagonal Length: Calculate the maximum possible diagonal length using the maximum height of 1818 inches.d2=5h2d^2 = 5h^2d2=5(18)2d^2 = 5(18)^2d2=5(324)d^2 = 5(324)d2=1620d^2 = 1620d=1620d = \sqrt{1620}d≈40.25 inchesd \approx 40.25 \text{ inches}
  6. Compare with Options: Compare the calculated diagonal length with the given options.\newlineThe calculated diagonal length is approximately 40.2540.25 inches, which is not an option. However, it is closest to option (B) 4242 inches, which is slightly larger than the calculated length. Since the TV must fit between the windows, the diagonal length must be less than or equal to the space available. Therefore, option (A) 3232 inches is the only possible size that is less than the calculated diagonal and also less than the space available between the windows.

More problems from Quantities that combine to zero: word problems

Question
Function g g can be thought of as a scaled version of f(x)=∣x∣ f(x)=|x| .\newlineWhat is the equation for g(x) g(x) ?\newlineChoose 11 answer:\newline(A) g(x)=−43∣x∣ g(x)=-\frac{4}{3}|x| \newline(B) g(x)=43∣x∣ g(x)=\frac{4}{3}|x| \newline(C) g(x)=−34∣x∣ g(x)=-\frac{3}{4}|x| \newline(D) g(x)=34∣x∣ g(x)=\frac{3}{4}|x|
Get tutor helpright-arrow

Posted 8 months ago

Question
The graph of y=∣x∣ y=|x| is reflected across the x x -axis and then scaled vertically by a factor of 53 \frac{5}{3} .\newlineWhat is the equation of the new graph?\newlineChoose 11 answer:\newline(A) y=−53∣x∣ y=-\frac{5}{3}|x| \newline(B) y=35∣x∣ y=\frac{3}{5}|x| \newline(C) y=−∣x−5∣+3 y=-|x-5|+3 \newline(D) y=∣x−3∣+5 y=|x-3|+5
Get tutor helpright-arrow

Posted 10 months ago

Question
Aiden has $200 \$ 200 with which to purchase hats and t-shirts that are to be sold at his class' next fundraiser. Each hat costs the same amount of money, and each t-shirt costs the same amount of money. If Aiden spends all his money entirely on hats, he will get 4040 hats. If Aiden purchases only t t -shirts, he will get 80 80 t\mathrm{t} -shirts. Which of the following best models the relationship between the number of hats, h h , and the number of t \mathrm{t} -shirts, t t , that Aiden could purchase with this money?\newlineChoose 11 answer:\newline(A) 40h+80t=400 40 h+80 t=400 \newline(B) 80h+40t=200 80 h+40 t=200 \newline(C) 5h+2.5t=200 5 h+2.5 t=200 \newline(D) 2.5h+5t=200 2.5 h+5 t=200
Get tutor helpright-arrow

Posted 10 months ago

Question
We want to find the intersection points of the graphs given by the following system of equations:\newline{x−y=−4y=5(x+1)2−3 \left\{\begin{array}{l} x-y=-4 \\ y=5(x+1)^{2}-3 \end{array}\right. \newlineOne of the intersection points is (−2,2) (-2,2) .\newlineFind the other intersection point. Your answer must be exact.
Get tutor helpright-arrow

Posted 10 months ago

Question
Derrick has 22 \mathbf{2 2} dollars. Colleen has x x dollars. Which of the following represents the total amount of money Derrick and Colleen have, in dollars?\newlineChoose 11 answer:\newline(A) x−22 x-22 \newline(B) x+22 x+22 \newline(C) 22x 22 x \newline(D) 22x+22 22 x+22
Get tutor helpright-arrow

Posted 10 months ago

Question
Wilber wants to make the pond in his backyard bigger. It is currently a cone with a radius of 3030 meters and a depth of 1515 meters. He wants to increase the radius to 4040 meters and the depth to 2020 meters. How much more water will the pond hold, in thousands of cubic meters?\newline(Round to the nearest thousand cubic meters.)
Get tutor helpright-arrow

Posted 4 months ago

Question
Ari thinks the perfect milkshake has 55 scoops of ice cream for every 33 spoonfuls of caramel. Freeze Zone makes batches of milkshakes with 1010 scoops of ice cream and 77 spoonfuls of caramel.\newlineWhat will Ari think about the amount of caramel in Freeze Zone's milkshakes?\newlineChoose 11 answer:\newline(A) Freeze Zone's milkshakes have too much caramel.\newline(B) Freeze Zone's milkshakes have too little caramel.\newline(C) Freeze Zone's milkshakes are just right.
Get tutor helpright-arrow

Posted 8 months ago

Question
Nayeli lights a 4 m2 4 \mathrm{~m}^{2} space with 1212 candles. Citlali lights a 10 m2 10 \mathrm{~m}^{2} space with 3030 of the same type of candles.\newlineWhose space is lit brighter?\newlineChoose 11 answer:\newline(A) Nayeli's area\newline(B) Citlali's area\newline(C) The spaces are equally bright.
Get tutor helpright-arrow

Posted 5 months ago

Question
Lashawn makes scrambled eggs with 33 spoonfuls of salsa for every 22 eggs. Gilberta adds 77 spoonfuls of salsa for every 55 eggs.\newlineWhose scrambled eggs have a stronger salsa taste?\newlineChoose 11 answer:\newline(A) Lashawn's eggs\newline(B) Gilberta's eggs\newline(C) The dishes of scrambled eggs have equal salsa tastes.
Get tutor helpright-arrow

Posted 8 months ago

Question
You pick a card at random, put it back, and then pick another card at random.\newline44\newline55\newline66\newline77\newlineWhat is the probability of picking a number greater than 55 and then picking a 44 ?\newlineWrite your answer as a percentage.
Get tutor helpright-arrow

Posted 1 month ago

View all (40)

Related topics

Algebra - Order of OperationsAlgebra - Distributive Property`X` and `Y` AxesGeometry - Scalene TriangleCommon MultipleGeometry - Quadrant