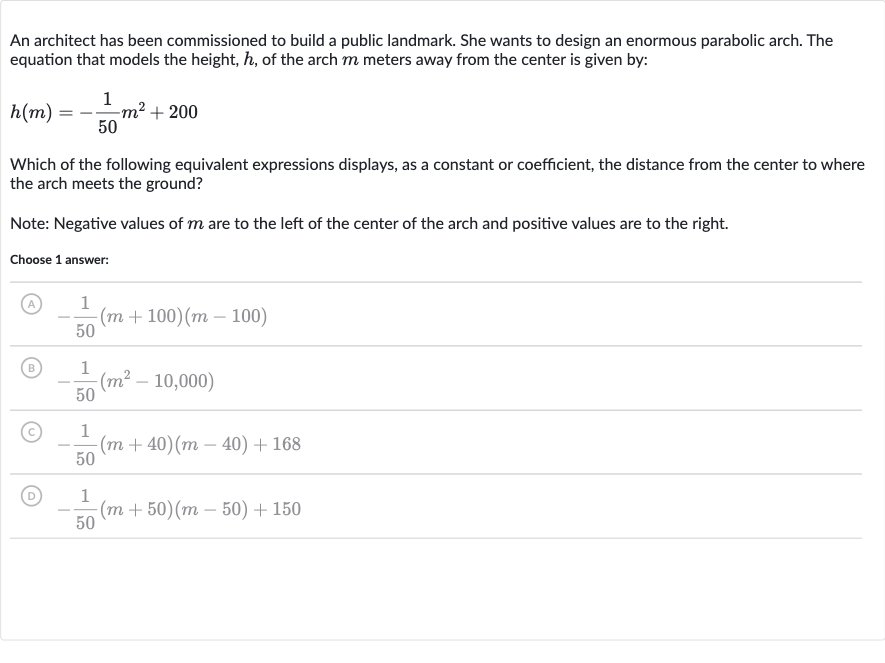
An architect has been commissioned to build a public landmark. She wants to design an enormous parabolic arch. The equation that models the height, h, of the arch m meters away from the center is given by: h(m)=-(1)/(50)m^(2)+200 Which of the following equivalent expressions displays, as a constant or coefficient, the distance from the center to where the arch meets the ground? Note: Negative values of m are to the left of the center of the arch and positive values are to the right. Choose 1 answer: (A) -(1)/(50)(m+100)(m-100) (B) -(1)/(50)(m^(2)-10,000) (C) -(1)/(50)(m+40)(m-40)+168 (D) -(1)/(50)(m+50)(m-50)+150

Question

An architect has been commissioned to build a public landmark. She wants to design an enormous parabolic arch. The equation that models the height,  h, of the arch  m meters away from the center is given by:  h(m)=-(1)/(50)m^(2)+200 Which of the following equivalent expressions displays, as a constant or coefficient, the distance from the center to where the arch meets the ground? Note: Negative values of  m are to the left of the center of the arch and positive values are to the right. Choose 1 answer: (A)  -(1)/(50)(m+100)(m-100) (B)  -(1)/(50)(m^(2)-10,000) (C)  -(1)/(50)(m+40)(m-40)+168 (D)  -(1)/(50)(m+50)(m-50)+150

Bytelearn · Accepted Answer

Analyze Equation: Analyze the given equation for the height of the arch. The equation given is h(m) = -(1/50)m^2 + 200. This is a parabolic equation in the form of h(m) = -a(m - h)^2 + k, where (h, k) is the vertex of the parabola. In this case, the vertex is at (0, 200), which means the arch is 200 meters high at the center.Determine Meeting Points: Determine the points where the arch meets the ground. The arch meets the ground when h(m) = 0. We need to solve the equation -(1/50)m^2 + 200 = 0 for m.Solve for m: Solve the equation for m. -(1/50)m^2 + 200 = 0 (1/50)m^2 = 200 m^2 = 200 * 50 m^2 = 10,000 m = ±√10,000 m = ±100 The arch meets the ground at m = 100 meters to the right of the center and m = -100 meters to the left of the center.Compare Solutions: Compare the solutions to the answer choices. We are looking for an expression that shows the distance from the center to where the arch meets the ground as a constant or coefficient. The solutions we found are m = ±100, which means the correct expression will have (m - 100) and (m + 100) as factors.Match Answer Choices: Match the solutions to the answer choices. The only answer choice that has (m - 100) and (m + 100) as factors is: (A) -(1/50)(m + 100)(m - 100) This choice correctly represents the distance from the center to where the arch meets the ground as a constant or coefficient.

Full solution

More problems from Power rule

Related topics