Translate the sentence into an equation. $\newline$ Twice the difference of a number and $5$ is $7$ . $\newline$ Use the variable $y$ for the unknown number.

Full solution

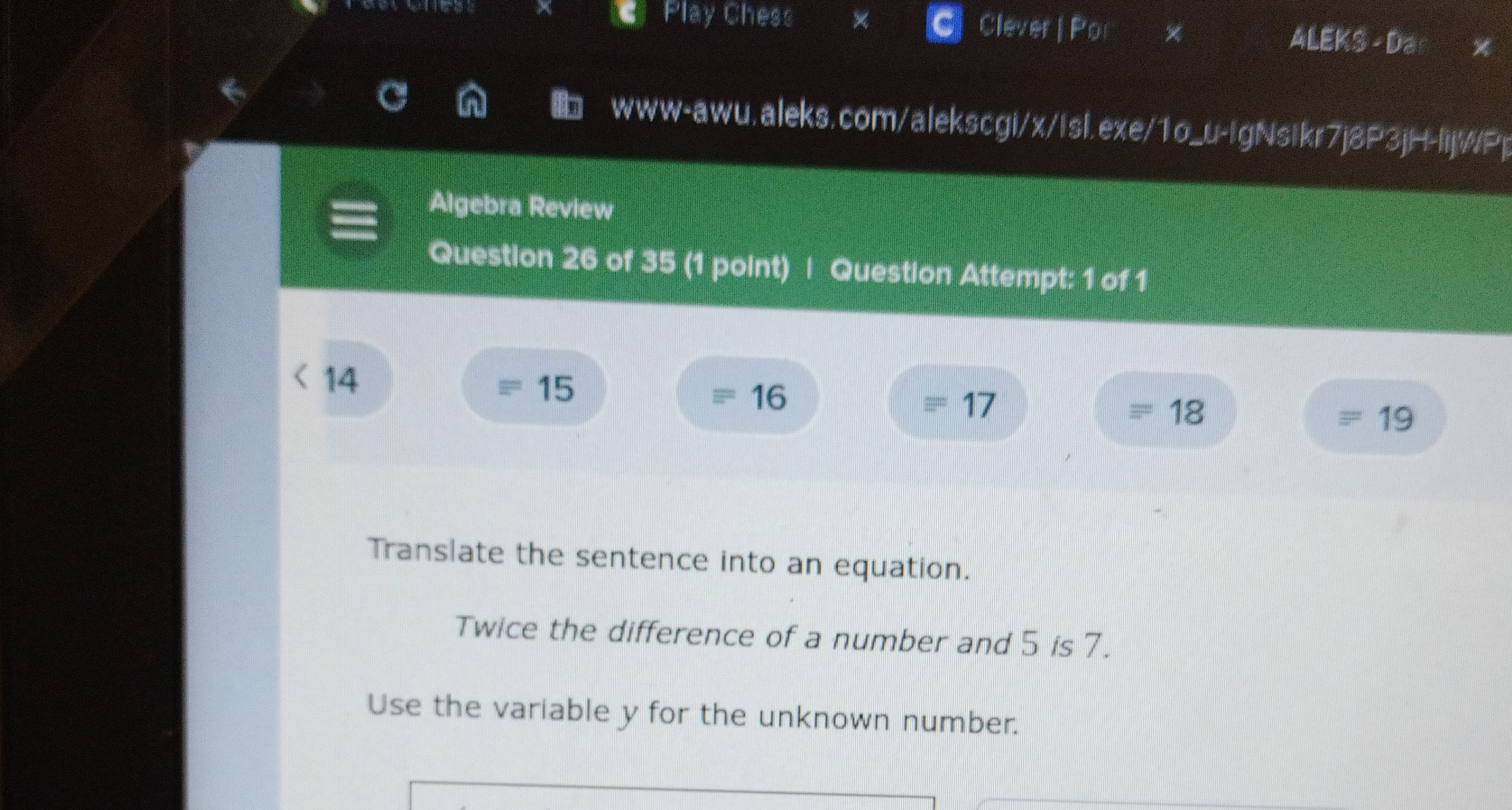
Q. Translate the sentence into an equation.

\newline

Twice the difference of a number and

5

7

\newline

Use the variable

y

for the unknown number.

Define Variable: Let's define the variable for the unknown number. We will use $y$ as the variable for the unknown number.
Translate into Equation: Now, let's translate the sentence into an equation. The sentence ＂Twice the difference of a number and $5$ is $7$ ＂ means we take the number $y$ , subtract $5$ from it, and then multiply the result by $2$ to get $7$ . This can be written as $2(y - 5) = 7$ .
Distribute and Simplify: To solve for $y$ , we first distribute the $2$ across the parentheses. This means we multiply $2$ by each term inside the parentheses: $2 \times y$ and $2 \times (-5)$ , which gives us $2y - 10$ .
Isolate Variable: Now we have the equation $2y - 10 = 7$ . The next step is to isolate $y$ by adding $10$ to both sides of the equation to cancel out the $-10$ on the left side. This gives us $2y = 7 + 10$ .
Solve for Variable: After adding $10$ to both sides, we get $2y = 17$ . Now, we divide both sides by $2$ to solve for $y$ . This gives us $y = \frac{17}{2}$ .
Solve for Variable: After adding $10$ to both sides, we get $2y = 17$ . Now, we divide both sides by $2$ to solve for $y$ . This gives us $y = \frac{17}{2}$ .Finally, we calculate $\frac{17}{2}$ to get the value of $y$ . The result is $y = 8.5$ .