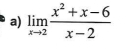Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

a) lim_(x rarr2)(x^(2)+x-6)/(x-2)

lim⁡x→2x2+x−6x−2 \lim _{x \rightarrow 2} \frac{x^{2}+x-6}{x-2} =

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Calculusright chevron icon
Find derivatives of using multiple formulaeright chevron icon

Full solution

Q. lim⁡x→2x2+x−6x−2 \lim _{x \rightarrow 2} \frac{x^{2}+x-6}{x-2} =
  1. Factorize the numerator: Simplify the expression in the numerator:\newline(x2+x−6)(x^2 + x - 6) can be factored into (x−2)(x+3)(x - 2)(x + 3).\newlineCalculation: x2+x−6=x2−2x+3x−6=(x(x−2)+3(x−2))=(x−2)(x+3)x^2 + x - 6 = x^2 - 2x + 3x - 6 = (x(x - 2) + 3(x - 2)) = (x - 2)(x + 3).
  2. Substitute factored form: Substitute the factored form back into the original limit expression: lim⁡x→2(x−2)(x+3)x−2\lim_{x \rightarrow 2}\frac{(x - 2)(x + 3)}{x - 2}. Calculation: (x−2)(x - 2) terms cancel out, leaving lim⁡x→2(x+3)\lim_{x \rightarrow 2}(x + 3).
  3. Evaluate the limit: Evaluate the limit of the simplified expression: lim⁡x→2(x+3)=2+3\lim_{x \rightarrow 2}(x + 3) = 2 + 3. Calculation: 2+3=52 + 3 = 5.

More problems from Find derivatives of using multiple formulae

Question
Find the derivative of f(x) f(x) .\newlinef(x)=cos⁡(x) f(x) = \cos(x) \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=tan⁡(x) f(x) = \tan(x) \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=ex f(x) = e^x \newlinef′(x)= f'\left(x\right) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=ln⁡(x) f(x) = \ln(x) \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=tan⁡−1x f(x) = \tan^{-1}{x} \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of f(x) f(x) .\newlinef(x)=xex f(x) = x e^x \newlinef′(x)= f'\left(x\right) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of f(x) f(x) . \newlinef(x)=exx f(x) = \frac{e^x}{x} \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of f(x) f(x) . \newline f(x)=e(x+1) f(x) = e^{(x + 1)} \newline f′(x)= f'\left(x\right) = ______
Get tutor helpright-arrow

Posted 1 month ago

Question
Find the derivative of f(x) f(x) . \newlinef(x)=x+3 f(x) = \sqrt{x+3} \newlinef′(x)= f'(x) = ______
Get tutor helpright-arrow

Posted 2 months ago

Question
Find the derivative of g(x) g(x). \newline g(x)=ln⁡(2x) g(x) = \ln(2x) \newline g′(x)= g^{\prime}(x) = ______
Get tutor helpright-arrow

Posted 3 months ago

View all (665)