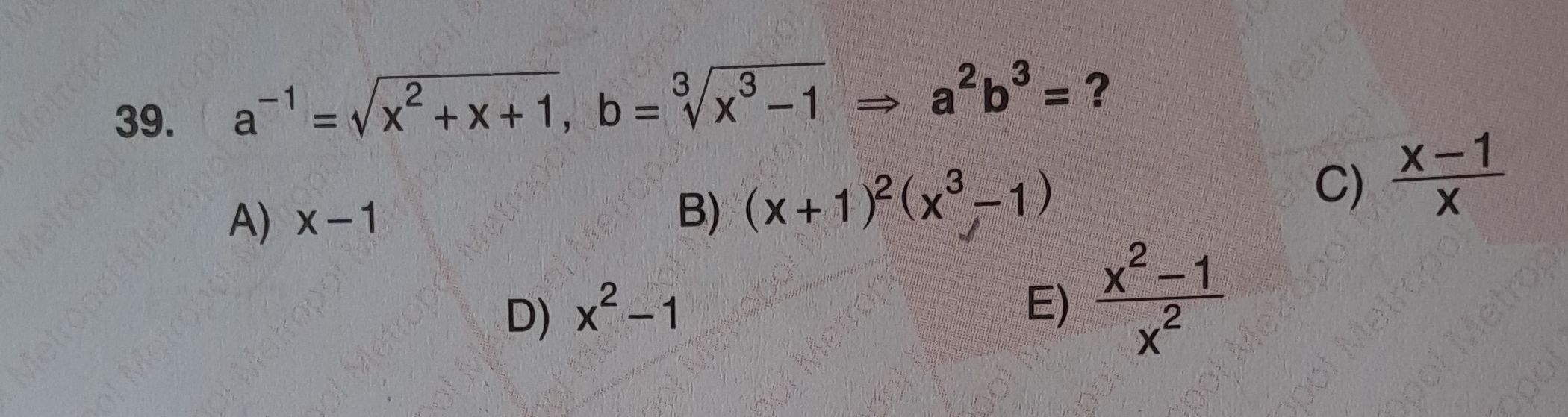a^(-1)=sqrt(x^(2)+x+1),b=root(3)(x^(3)-1)=a^(2)b^(3)= ? A) x-1 B) (x+1)^(2)(x^(3)-1) C) (x-1)/(x) D) x^(2)-1 E) (x^(2)-1)/(x^(2))

Question

a^(-1)=sqrt(x^(2)+x+1),b=root(3)(x^(3)-1)=>a^(2)b^(3)= ? A)  x-1 B)  (x+1)^(2)(x^(3)-1) C)  (x-1)/(x) D)  x^(2)-1 E)  (x^(2)-1)/(x^(2))

Bytelearn · Accepted Answer

Find a^2 Expression: First, we need to find the expression for $ a^2 $ given that $ a^{-1} = \sqrt{x^2 + x + 1} $. To find $ a^2 $, we can take the reciprocal of $ a^{-1} $ and then square it. $ a = \frac{1}{\sqrt{x^2 + x + 1}} $ $ a^2 = \left(\frac{1}{\sqrt{x^2 + x + 1}}\right)^2 $ $ a^2 = \frac{1}{x^2 + x + 1} $Find b^3 Expression: Next, we need to find the expression for $ b^3 $ given that $ b = \sqrt[3]{x^3 - 1} $. To find $ b^3 $, we simply cube $ b $. $ b^3 = \left(\sqrt[3]{x^3 - 1}\right)^3 $ $ b^3 = x^3 - 1 $Multiply a^2 and b^3: Now, we need to multiply $ a^2 $ and $ b^3 $ to find $ a^2 b^3 $. $ a^2 b^3 = \left(\frac{1}{x^2 + x + 1}\right) \cdot (x^3 - 1) $Simplify the Expression: We can simplify the expression by multiplying the numerator of $ a^2 $ with $ b^3 $. $ a^2 b^3 = \frac{x^3 - 1}{x^2 + x + 1} $Check for Further Simplification: We need to check if the expression $ \frac{x^3 - 1}{x^2 + x + 1} $ can be simplified further or matches any of the given options. However, the denominator $ x^2 + x + 1 $ does not factor easily, and there is no obvious common factor between the numerator and the denominator. Therefore, the expression is already in its simplest form.

$39$ . $a^{-1}=\sqrt{x^{2}+x+1}, b=\sqrt[3]{x^{3}-1} \Rightarrow a^{2} b^{3}=$ ? $\newline$ A) $x-1$ $\newline$ B) $(x+1)^{2}\left(x^{3}-1\right)$ $\newline$ C) $\frac{x-1}{x}$ $\newline$ D) $x^{2}-1$ $\newline$ E) $\frac{x^{2}-1}{x^{2}}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics