Which of the following radian measures is equal to $315^{\circ}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{5 \pi}{4}$ radians $\newline$ B $\frac{7 \pi}{4}$ radians $\newline$ (C) $\frac{9 \pi}{4}$ radians $\newline$ (D) $\frac{11 \pi}{4}$ radians

View step-by-step help

Home

Math Problems

Algebra 2

Convert between radians and degrees

Full solution

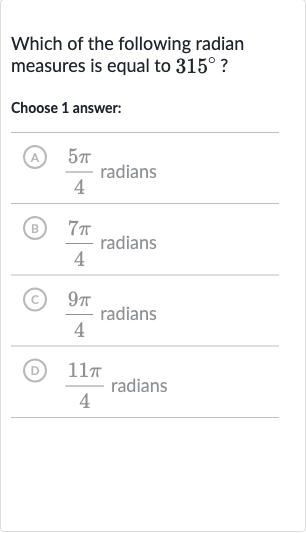
Q. Which of the following radian measures is equal to

315^{\circ}

\newline

Choose

1

answer:

\newline

(A)

\frac{5 \pi}{4}

radians

\newline

\frac{7 \pi}{4}

radians

\newline

(C)

\frac{9 \pi}{4}

radians

\newline

(D)

\frac{11 \pi}{4}

radians

Identify formula for conversion: Identify the formula to convert degrees to radians. The formula is $\text{radians} = \text{degrees} \times \left(\frac{\pi}{180^\circ}\right)$ .
Convert $315$ degrees to radians: Convert $315$ degrees into radians using the formula. By substituting $315$ degrees into the formula, we get $315^\circ \times \left(\frac{\pi}{180^\circ}\right) = \left(\frac{315}{180}\right) \times \pi = \left(\frac{7}{4}\right) \times \pi$ radians.
Simplify fraction $(\frac{315}{180}):</b> Simplify the fraction \$(\frac{315}{180})$ to its lowest terms. Dividing both the numerator and the denominator by $45$ , we get $(\frac{7}{4})$ .
Choose correct option for $315$ degrees: Choose the correct option of radians for $315$ degrees. The correct option is $(\frac{7}{4}) \times \pi$ radians, which is equivalent to $315$ degrees.

More problems from Convert between radians and degrees

Question
Find the measure of a negative angle coterminal with $180^\circ$ . $\newline$ ____ $^\circ$
Get tutor help
Posted 3 months ago

Question
Find the measure of the reference angle for a $170^\circ$ angle.
Get tutor help
Posted 2 months ago

Question
How many radians is $60^\circ$ ? $\newline$ Choices: $\newline$ $[A]\frac{\pi}{3}\text{ radians}$ $\newline$ $[B]\frac{\pi}{2}\text{ radians}$ $\newline$ $[C]\frac{\pi}{4}\text{ radians}$ $\newline$ $[D]\frac{\pi}{6}\text{ radians}$
Get tutor help
Posted 3 months ago

Question
Which of the following radian measures is equal to $90^{\circ}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{\pi}{3}$ radians $\newline$ B $\frac{\pi}{4}$ radians $\newline$ (C) $\frac{\pi}{2}$ radians $\newline$ (D) $\frac{\pi}{6}$ radians
Get tutor help
Posted 2 months ago

Question
Which of the following radian measures is equal to $225^{\circ}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{\pi}{4}$ radians $\newline$ B $\frac{\pi}{2}$ radians $\newline$ (C) $\frac{3 \pi}{4}$ radians $\newline$ (D) $\frac{5 \pi}{4}$ radians
Get tutor help
Posted 4 months ago

Question
Which of the following radian measures is equal to $135^{\circ}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{\pi}{4}$ radians $\newline$ (B) $\frac{\pi}{2}$ radians $\newline$ (C) $\frac{3 \pi}{4}$ radians $\newline$ (D) $\pi$ radians
Get tutor help
Posted 4 months ago

Question
Which of the following radian measures is equal to $330^{\circ}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{15 \pi}{6}$ radians $\newline$ B $\frac{7 \pi}{6}$ radians $\newline$ (C) $\frac{11 \pi}{6}$ radians $\newline$ (D) $\frac{13 \pi}{6}$ radians
Get tutor help
Posted 4 months ago

Question
Which of the following radian measures is equal to $75^{\circ}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{\pi}{12}$ radians $\newline$ B $\frac{\pi}{3}$ radians $\newline$ (C) $\frac{5 \pi}{12}$ radians $\newline$ (D) $\frac{7 \pi}{12}$ radians
Get tutor help
Posted 2 months ago

Question
Which of the following radian measures is equal to $240^{\circ}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{4 \pi}{3}$ radians $\newline$ B $\frac{5 \pi}{3}$ radians $\newline$ (C) $\frac{7 \pi}{3}$ radians $\newline$ (D) $\frac{11 \pi}{3}$ radians
Get tutor help
Posted 4 months ago

Question
Which of the following radian measures is equal to $120^{\circ}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{2 \pi}{3}$ radians $\newline$ (B) $\pi$ radians $\newline$ (C) $\frac{4 \pi}{3}$ radians $\newline$ (D) $\frac{5 \pi}{3}$ radians
Get tutor help
Posted 4 months ago

View all (43)

Which of the following radian measures is equal to 315∘ 315^{\circ} 315∘ ?\newlineChoose 111 answer:\newline(A) 5π4 \frac{5 \pi}{4} 45π​ radians\newlineB 7π4 \frac{7 \pi}{4} 47π​ radians\newline(C) 9π4 \frac{9 \pi}{4} 49π​ radians\newline(D) 11π4 \frac{11 \pi}{4} 411π​ radians

Which of the following radian measures is equal to $315^{\circ}$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{5 \pi}{4}$ radians $\newline$ B $\frac{7 \pi}{4}$ radians $\newline$ (C) $\frac{9 \pi}{4}$ radians $\newline$ (D) $\frac{11 \pi}{4}$ radians