Full solution
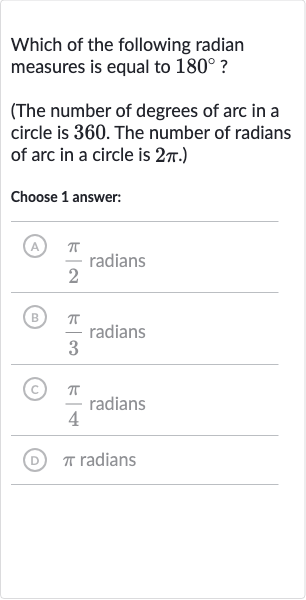
Q. Which of the following radian measures is equal to ?(The number of degrees of arc in a circle is . The number of radians of arc in a circle is .)Choose answer:(A) radians(B) radiansC) radians(D) radians
- Understanding degrees and radians: Understand the relationship between degrees and radians. We know that degrees is equal to radians. Therefore, to convert degrees to radians, we use the formula .
- Converting degrees to radians: Convert degrees into radians using the formula from Step . By substituting degrees into the formula, we get degrees radians.
- Choosing the correct option for degrees: Choose the correct option of radians for degrees. The correct option is radians, which is equivalent to degrees.
More problems from Convert between radians and degrees
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help