AI tutor
Welcome to Bytelearn!
Let’s check out your problem:
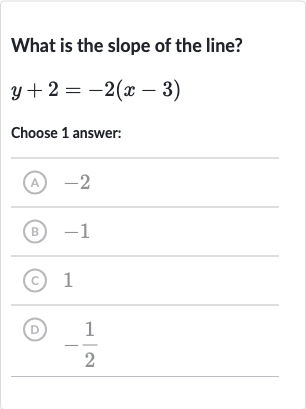
What is the slope of the line?Choose answer:(A) (B) (C) (D)
Full solution
Q. What is the slope of the line?Choose answer:(A) (B) (C) (D)
- Rewriting the equation: First, we need to rewrite the equation in slope-intercept form, which is , where is the slope and is the y-intercept.
- Distributing the : Now, distribute the to both terms inside the parentheses.
- Isolating y: Next, we subtract from both sides to isolate on one side of the equation.
- Combining constant terms: Combine the constant terms on the right side of the equation.
- Identifying the slope: Now that the equation is in slope-intercept form, we can identify the slope directly from the equation. The coefficient of is the slope of the line.The slope of the line is .
More problems from Solve linear equations: mixed review
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
