AI tutor
Full solution
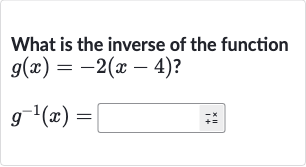
Q. What is the inverse of the function
- Replace with : To find the inverse of the function , we first replace with to make the equation easier to manipulate. So we have .
- Swap and : Next, we swap and to find the inverse. This gives us .
- Solve for y: Now, we solve for y. Start by dividing both sides by to isolate the term with y. This gives us .
- Add to both sides: Next, add to both sides to solve for . This gives us .
- Inverse function expression: The expression we have now represents the inverse function. So, .