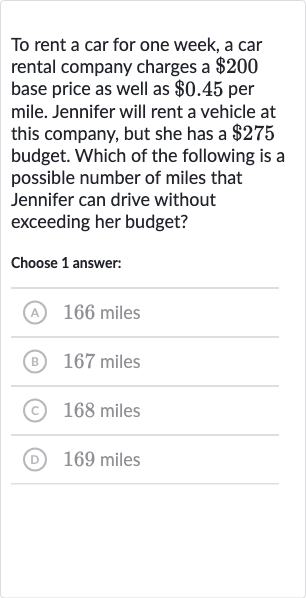
To rent a car for one week, a car rental company charges a $\$ 200$ base price as well as $\$ 0.45$ per mile. Jennifer will rent a vehicle at this company, but she has a $\$ 275$ budget. Which of the following is a possible number of miles that Jennifer can drive without exceeding her budget? $\newline$ Choose $1$ answer: $\newline$ (A) $\mathbf{1 6 6}$ miles $\newline$ (B) $\mathbf{1 6 7}$ miles $\newline$ (C) $\mathbf{1 6 8}$ miles $\newline$ (D) $\mathbf{1 6 9}$ miles

Full solution

Q. To rent a car for one week, a car rental company charges a

\$ 200

base price as well as

\$ 0.45

per mile. Jennifer will rent a vehicle at this company, but she has a

\$ 275

budget. Which of the following is a possible number of miles that Jennifer can drive without exceeding her budget?

\newline

Choose

1

answer:

\newline

(A)

\mathbf{1 6 6}

miles

\newline

(B)

\mathbf{1 6 7}

miles

\newline

(C)

\mathbf{1 6 8}

miles

\newline

(D)

\mathbf{1 6 9}

miles

Calculate Remaining Budget: Determine the remaining budget after the base price is subtracted. $\newline$ Jennifer has a $\$275$ budget and the base price for renting the car is $\$200$ . $\newline$ $\$275 - \$200 = \$75$ $\newline$ Remaining budget for miles: $\$75$
Determine Maximum Miles: Calculate the maximum number of miles Jennifer can drive with the remaining budget. The cost per mile is \$$0$.$45$. To find out how many miles she can drive, divide the remaining budget by the cost per mile. \$$75$ \div \$$0$.$45$ per mile = $166$.$666$... Jennifer can drive a maximum of $166.666\ldots$ miles with her remaining budget.
Round Down to Nearest Mile: Since Jennifer cannot drive a fraction of a mile, we need to round down to the nearest whole number.$\newline$The possible number of miles she can drive without exceeding her budget is $166$ miles.