AI tutor
Full solution
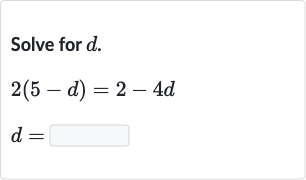
Q. Solve for .
- Simplify expression using distributive property: Simplify by using the distributive property.
- Set expression equal to other side of equation: Set the simplified expression equal to the other side of the equation.
- Add d to both sides: Add to both sides to get all the terms on one side.
- Isolate the term: Add to both sides to isolate the
d term.\newline 10 10 2 2 2 2 2 2 2 2 \newline 10 10 2 2 2 2 - Subtract
2 2 2 2 d d 10 + 2 d − 2 = 2 − 2 10 + 2d - 2 = 2 - 2 8 + 2 d = 0 8 + 2d = 0 - Divide both sides by
2 2 2 2 d d 8 + 2 d 2 = 0 2 \frac{8 + 2d}{2} = \frac{0}{2} 4 + d = 0 4 + d = 0 - Subtract
4 4 4 4 \newline 4 + d − 4 = 0 − 4 4 + d - 4 = 0 - 4 \newline d = − 4 d = -4
More problems from Solve multi-step linear equations
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help