Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

Simplify.
Rewrite the expression in the form
9^(n).

(9^(-3))/(9^(12))=◻++^(-x)

Simplify. $\newline$ Rewrite the expression in the form $9^{n}$ . $\newline$ $\frac{9^{-3}}{9^{12}}=\square$

View step-by-step help

View step-by-step help

Evaluate expressions using properties of exponents

Full solution

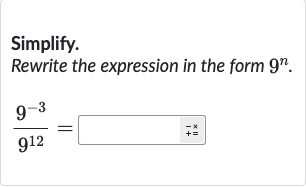
Q. Simplify.

\newline

Rewrite the expression in the form

9^{n}

.

\newline

\frac{9^{-3}}{9^{12}}=\square

Identify base and exponents: Identify the base and the exponents of both the numerator and the denominator. In the numerator, the base is $9$ raised to the exponent $-3$ . In the denominator, the base is $9$ raised to the exponent $12$ . $\newline$ Base: $9$ $\newline$ Exponent of numerator: $-3$ $\newline$ Exponent of denominator: $12$
Apply quotient rule for exponents: Apply the quotient rule for exponents, which states that when dividing like bases, you subtract the exponents. Rewrite the expression as a single power of $9$ . $\newline$ $\left(9^{-3}\right)/\left(9^{12}\right) = 9^{-3 - 12}$
Perform subtraction of exponents: Perform the subtraction of the exponents. $\newline$ $9^{(-3 - 12)} = 9^{-15}$
Verify expression form: Verify that the expression is now in the form of $9^{(n)}$ , where $n$ is the exponent. $\newline$ The expression is now $9^{(-15)}$ , which is in the form of $9^{(n)}$ with $n = -15$ .

More problems from Evaluate expressions using properties of exponents

Question

Write the expression using an exponent.

\newline

2 \times 2

\newline

Posted 3 months ago

Question

Evaluate the expression.

4 - 4^2

Posted 3 months ago

Question

x^2 = 4

Posted 2 months ago

Question

x^2 = 9

Posted 4 months ago

Question

\newline

x^2 = 0

\newline

Write your answer in simplified, rationalized form.

\newline

x =

x =

Posted 4 months ago

Question

x

\newline

8 = 2^x

\newline

x =

Posted 4 months ago

Question

x

\newline

6 = 7^x

\newline

x =

Posted 4 months ago

Question

Select the equivalent expression.

\newline

((8^{-5})/(2^{-2}))^{-4}=?

\newline

1

\newline

\newline

(8^{20})/(2^{8})

\newline

\newline

(2^{6})/(8^{9})

\newline

\newline

(1)/(8\cdot 2^{2})

Posted 15 days ago

Question

Select the equivalent expression.

\newline

\left(\frac{b^{7}}{4^{5}}\right)^{-3}=\,?

\newline

1

\newline

\frac{b^{21}}{4^{15}}

\newline

\frac{4^{15}}{b^{21}}

\newline

b^{-21}\cdot 4^{-15}

Posted 2 months ago

Question

Select the equivalent expression.

\newline

(3^{3}\cdot6^{6})^{-3}=

\newline

1

\newline

\frac{1}{3^{9}\cdot6^{18}}

\newline

\frac{6^{18}}{3^{9}}

\newline

\frac{3^{9}}{6^{18}}

Posted 2 months ago