Select the equivalent expression. $\newline$ $\left(\frac{z^{4}}{6^{2}}\right)^{-3}=$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{z}{6^{-1}}$ $\newline$ (B) $z^{12}\cdot 6^{6}$ $\newline$ (C) $\frac{6^{6}}{z^{12}}$

Full solution

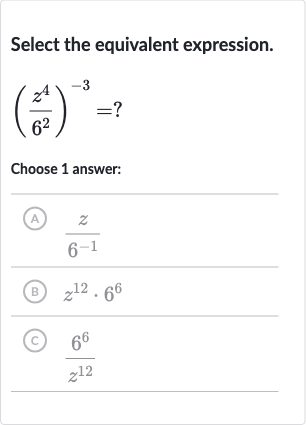
Q. Select the equivalent expression.

\newline

\left(\frac{z^{4}}{6^{2}}\right)^{-3}=

\newline

Choose

1

answer:

\newline

(A)

\frac{z}{6^{-1}}

\newline

(B)

z^{12}\cdot 6^{6}

\newline

(C)

\frac{6^{6}}{z^{12}}

Understand Exponent Properties: Understand the properties of exponents. When an expression with a power is raised to another power, we multiply the exponents. Also, a negative exponent means we take the reciprocal of the base and make the exponent positive.
Apply Exponent Rule: Apply the exponent rule to the given expression. $\newline$ $\left(\frac{z^{4}}{6^{2}}\right)^{-3}$ means we multiply the exponents of $z$ and $6$ by $-3$ . $\newline$ $\frac{z^{4 \cdot -3}}{6^{2 \cdot -3}}$
Calculate New Exponents: Calculate the new exponents. $\newline$ $z^{4 \times -3}$ becomes $z^{-12}$ and $6^{2 \times -3}$ becomes $6^{-6}$ . $\newline$ $\frac{z^{-12}}{6^{-6}}$
Rewrite with Positive Exponents: Rewrite the expression with positive exponents. $\newline$ To make the exponents positive, we take the reciprocal of each base. $\newline$ $\frac{6^{6}}{z^{12}}$
Match with Options: Match the simplified expression with the given options. $\newline$ The expression we have found, $(6^{6})/(z^{12})$ , matches option (C).