Full solution
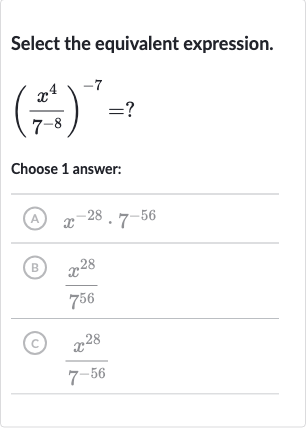
Q. Select the equivalent expression.?Choose answer:(A) (B) (C)
- Apply Quotient Rule: Apply the power of a quotient rule.The power of a quotient rule states that . We will apply this rule to the given expression .
- Simplify Exponents: Simplify the exponents.When raising a power to a power, you multiply the exponents. So, becomes and becomes .
- Write Final Expression: Write the final expression.The simplified expression is , which corresponds to one of the answer choices.
More problems from Evaluate expressions using properties of exponents
QuestionGet tutor help