Full solution
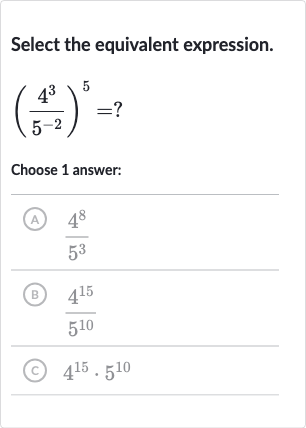
Q. Select the equivalent expression.Choose answer:(A) (B) (C)
- Apply Power Rule: Apply the power of a power rule.The power of a power rule states that . We will apply this rule to both the numerator and the denominator separately.
- Multiply Exponents: Perform the multiplication for the exponents.Now we multiply the exponents by .
- Rewrite Expression: Rewrite the expression with the new exponents.We now have the expression .
- Simplify Exponents: Simplify the expression by converting the negative exponent to a positive exponent.A negative exponent means that the base is on the wrong side of the fraction line, so we flip it to the other side to make the exponent positive.
- Choose Correct Answer: Choose the correct answer.The expression matches answer choice (C).
More problems from Evaluate expressions using properties of exponents
QuestionGet tutor help