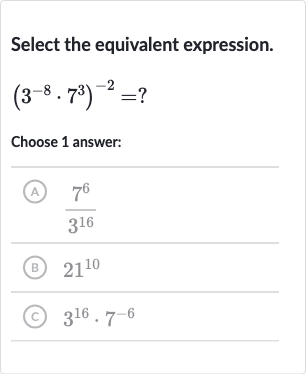
Select the equivalent expression. (3^(-8)*7^(3))^(-2)=? Choose 1 answer: (A) (7^(6))/(3^(16)) (B) 21^(10) (c) 3^(16)*7^(-6)

Question

Select the equivalent expression.  (3^(-8)*7^(3))^(-2)=? Choose 1 answer: (A)  (7^(6))/(3^(16)) (B)  21^(10) (c)  3^(16)*7^(-6)

Bytelearn · Accepted Answer

Apply product rule: Apply the power of a product rule, which states that (ab)^n = a^n * b^n, to the given expression (3^(-8)*7^(3))^(-2). (3^(-8)*7^(3))^(-2) = (3^(-8))^(-2) * (7^(3))^(-2)Apply power of a power rule: Apply the power of a power rule, which states that (a^m)^n = a^(m*n), to both parts of the expression. (3^(-8))^(-2) = 3^((-8)*(-2)) = 3^(16) (7^(3))^(-2) = 7^((3)*(-2)) = 7^(-6)Combine results: Combine the results from Step 2 to form the final expression. 3^(16) * 7^(-6)Rewrite as division: Recognize that 7^(-6) is the reciprocal of 7^(6), which means we can rewrite the expression as a division. 3^(16) * 7^(-6) = 3^(16) / 7^(6)Check answer choices: Check the answer choices to see which one matches the expression we have derived. (A) (7^(6))/(3^(16)) is not correct because the bases are flipped and the exponents are in the wrong places. (B) 21^(10) is not correct because it does not represent the bases 3 and 7 separately and the exponents are incorrect. (C) 3^(16)*7^(-6) is correct because it matches the expression we have derived.

Select the equivalent expression. $\newline$ $(3^{-8}\cdot7^{3})^{-2}=$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{7^{6}}{3^{16}}$ $\newline$ (B) $21^{10}$ $\newline$ (C) $3^{16}\cdot7^{-6}$

Full solution

More problems from Evaluate expressions using properties of exponents

Related topics

Select the equivalent expression.\newline(3−8⋅73)−2=(3^{-8}\cdot7^{3})^{-2}=(3−8⋅73)−2=?\newlineChoose 111 answer:\newline(A) 76316\frac{7^{6}}{3^{16}}31676​\newline(B) 211021^{10}2110\newline(C) 316⋅7−63^{16}\cdot7^{-6}316⋅7−6

Select the equivalent expression. $\newline$ $(3^{-8}\cdot7^{3})^{-2}=$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{7^{6}}{3^{16}}$ $\newline$ (B) $21^{10}$ $\newline$ (C) $3^{16}\cdot7^{-6}$