Full solution
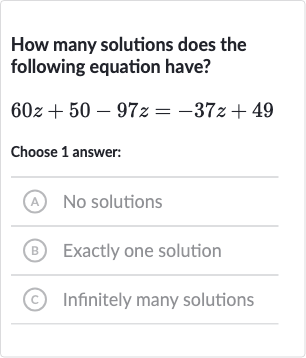
Q. How many solutions does the following equation have?Choose answer:(A) No solutions(B) Exactly one solution(C) Infinitely many solutions
- Combine like terms: Combine like terms on both sides of the equation.Combine the terms on the left side: This simplifies to:
- Isolate the variable : Attempt to isolate the variable on one side.However, we notice that the terms on both sides of the equation are the same, . This means that if we subtract
− 37 -37 z terms will cancel out.\newline − 37 -37 50 50 − 37 -37 − 37 -37 49 49 − 37 -37 \newline 50 50 49 49 - Analyze the resulting statement: Analyze the resulting statement.
\newline 50 = 49 50 = 49 z z
More problems from Find the number of solutions to a linear equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help