Full solution
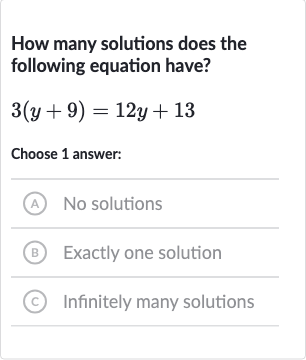
Q. How many solutions does the following equation have?Choose answer:(A) No solutions(B) Exactly one solution(C) Infinitely many solutions
- Distribute the : Distribute the on the left side of the equation to both and .
= - Rewrite the equation: Rewrite the equation with the distributed terms.
- Move terms involving : Move all terms involving to one side of the equation and constants to the other side.Subtract from both sides:
- Subtract : Subtract from both sides to isolate the term with .
- Divide both sides: Divide both sides by to solve for .
- Check the solution: Check if the solution is valid by substituting back into the original equation.
More problems from Find the number of solutions to a linear equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help