Full solution
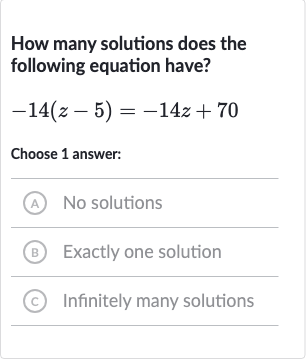
Q. How many solutions does the following equation have?Choose answer:(A) No solutions(B) Exactly one solution(C) Infinitely many solutions
- Distribute : Distribute to both terms inside the parentheses.
- Compare distributed form: Compare the distributed form of the equation to the right side of the original equation.The distributed form is , and the right side of the original equation is also .
- Equation has infinitely many solutions: Since both sides of the equation are identical, the equation is true for all values of .This means the equation has infinitely many solutions.
More problems from Find the number of solutions to a linear equation
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help