AI tutor
Full solution
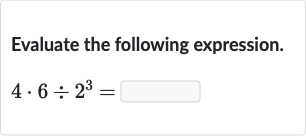
Q. Evaluate the following expression.
- Identify order of operations: Identify the order of operations.According to the order of operations (PEMDAS/BODMAS), we first evaluate any expressions inside parentheses, then exponents, followed by multiplication and division from left to right, and finally addition and subtraction from left to right.In the expression , there are no parentheses to consider, but there is an exponent (), which we should evaluate first.
- Calculate exponent value: Calculate the value of the exponent. means is multiplied by itself times.
- Substitute exponent value: Substitute the value of the exponent back into the expression.Now the expression becomes .
- Perform multiplication: Perform the multiplication.Next, we perform the multiplication operation before division.Now the expression is simplified to .
- Perform division: Perform the division.Finally, we divide by .
More problems from Powers with negative bases
QuestionGet tutor help