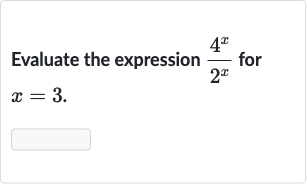AI tutor
Full solution
Q. Evaluate the expression for .
- Recognize the base: Recognize that can be expressed as squared, so .
- Apply power of a power rule: Apply the power of a power rule, which states that . Therefore, .
- Substitute with : Substitute with into the expression to get which simplifies to .
- Apply quotient rule for exponents: Now we have the expression . Apply the quotient rule for exponents, which states that when .
- Subtract the exponents: Subtract the exponents: . So, .
- Calculate the final answer: Calculate to get the final answer. .