Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

A circle has a circumference of
4pi feet (ft). An arc,
x, in this circle has a central angle of
240^(@). What is the length of
x ?
Choose 1 answer:
(A)
(4pi)/(3)ft
(B)
(8pi)/(3)ft
(C)
480ft
(D)
960ft

A circle has a circumference of $4 \pi$ feet (ft). An arc, $x$ , in this circle has a central angle of $240^{\circ}$ . What is the length of $x$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $\frac{4 \pi}{3} \mathrm{ft}$ $\newline$ (B) $\frac{8 \pi}{3} \mathrm{ft}$ $\newline$ (C) $480 \mathrm{ft}$ $\newline$ (D) $960 \mathrm{ft}$

View step-by-step help

View step-by-step help

Scale drawings: word problems

Full solution

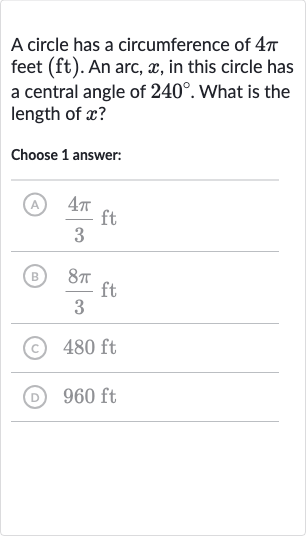
Q. A circle has a circumference of

4 \pi

feet (ft). An arc,

x

, in this circle has a central angle of

240^{\circ}

. What is the length of

x

?

\newline

Choose

1

answer:

\newline

(A)

\frac{4 \pi}{3} \mathrm{ft}

\newline

(B)

\frac{8 \pi}{3} \mathrm{ft}

\newline

(C)

480 \mathrm{ft}

\newline

(D)

960 \mathrm{ft}

Circumference Calculation: The circumference $C$ of a circle is related to its radius $r$ by the formula $C = 2\pi r$ . We are given that the circumference is $4\pi$ ft, so we can solve for $r$ : $\newline$ $4\pi = 2\pi r$ $\newline$ $r = 2$ ft
Central Angle Conversion: The length of an arc $s$ in a circle is given by the formula $s = r\theta$ , where $\theta$ is the central angle in radians. To use this formula, we need to convert the central angle from degrees to radians. The conversion factor is $\pi$ radians = $180^\circ$ , so: $\newline$ $\theta = 240^\circ \times (\pi/180^\circ) = (4/3)\pi$ radians
Arc Length Calculation: Now we can calculate the length of the arc $x$ using the radius we found in step $1$ and the angle in radians from step $2$ : $s = r\theta = 2 \, \text{ft} \times \left(\frac{4}{3}\right)\pi = \left(\frac{8}{3}\right)\pi \, \text{ft}$

More problems from Scale drawings: word problems

Question

\newline

1,000

\text{ milligrams}

\_\_\_\_

\text{ grams}

Posted 3 months ago

Question

3

-gallon bottle of bleach costs

\$11.52

. What is the price per quart?

\newline

Posted 3 months ago

Question

Maureen can't wait to make chocolate chip zucchini bread with zucchini from her garden. Her recipe calls for

8

ounces of chocolate chips per loaf. If she has enough zucchini to make

4

loaves of zucchini bread, how many pounds of chocolate chips does she need?

\newline

Hint: There are

16

1

\newline

Write your answer as a whole number, decimal, or simplified fraction. Do not round.

\newline

Posted 3 months ago

Question

A whale is swimming due north at a speed of

30

miles per hour. Just

5

miles away, a whale-watching tour boat is traveling south, directly toward the whale, at a speed of

46

miles per hour. How long will it be before they meet? If necessary, round your answer to the nearest minute.

\_\_\_\_

\_\_\_\_

Posted 3 months ago

Question

\newline

500

=

Posted 4 months ago

Question

\newline

2,000

=

Posted 4 months ago

Question

\newline

750

=

Posted 4 months ago

Question

\newline

1,500

=

Posted 4 months ago

Question

\newline

1,500

=

Posted 4 months ago

Question

The formula for the size of a file that was downloaded over time

t

and at an average rate

r

r \cdot t

. Siena downloaded a file at a rate of

800 \text{ kilobytes per second}

110 \text{ seconds}

. What calculation will give us the estimated size of the file Siena downloaded, in megabytes? Choose

1

\newline

800 \cdot 110 \cdot 60

\newline

800 \cdot \frac{110}{60}

\newline

800 \cdot 1000 \cdot 110

\newline

\frac{800}{1000} \cdot 110

Posted 3 months ago