Resources

Resources

Bytelearn - cat image with glasses

AI tutor

Welcome to Bytelearn!

Let’s check out your problem:

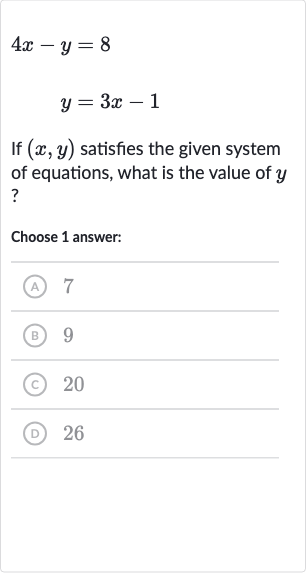
4x-y=8

y=3x-1
If
(x,y) satisfies the given system of equations, what is the value of
y ?
Choose 1 answer:
(A) 7
(B) 9
(C) 20
(D) 26

$4 x-y=8$ $\newline$ $y=3 x-1$ $\newline$ If $(x, y)$ satisfies the given system of equations, what is the value of $y$ ? $\newline$ Choose $1$ answer: $\newline$ (A) $7$ $\newline$ (B) $9$ $\newline$ (C) $\mathbf{2 0}$ $\newline$ (D) $26$

View step-by-step help

View step-by-step help

Solve linear equations: mixed review

Full solution

Q.

4 x-y=8

\newline

y=3 x-1

\newline

If

(x, y)

satisfies the given system of equations, what is the value of

y

?

\newline

Choose

1

answer:

\newline

(A)

7

\newline

(B)

9

\newline

(C)

\mathbf{2 0}

\newline

(D)

26

Write Equations: Write down the given system of equations. $\newline$ The system of equations is: $\newline$ $4x - y = 8$ $\newline$ $y = 3x - 1$
Substitute and Simplify: Substitute the expression for $y$ from the second equation into the first equation. $\newline$ Since $y = 3x - 1$ , we can replace $y$ in the first equation with $3x - 1$ . $\newline$ $4x - (3x - 1) = 8$
Solve for x: Solve for x. $\newline$ Distribute the negative sign in the first equation and combine like terms. $\newline$ $4x - 3x + 1 = 8$ $\newline$ $x + 1 = 8$ $\newline$ Subtract $1$ from both sides. $\newline$ $x = 8 - 1$ $\newline$ $x = 7$
Substitute for y: Substitute the value of $x$ back into the second equation to find $y$ . We know that $y = 3x - 1$ , so we substitute $x = 7$ . $y = 3(7) - 1$ $y = 21 - 1$ $y = 20$

More problems from Solve linear equations: mixed review

Question

\newline

(\frac{3}{4})x= 12

\newline

x =

Posted 8 months ago

Question

\newline

-\frac{5}{9}x= 15

\newline

x =

Posted 7 months ago

Question

How many solutions does the following equation have?

\newline

5x+8-7x=-4x+1

\newline

1

\newline

(A) No solutions

\newline

(B) Exactly one solution

\newline

(C) Infinitely many solutions

Posted 10 months ago

Question

How many solutions does the following equation have?

\newline

-2z+10+7z=16z+7

\newline

1

\newline

(A) No solutions

\newline

(B) Exactly one solution

\newline

(C) Infinitely many solutions

Posted 5 months ago

Question

How many solutions does the following equation have?

\newline

7(y-8)=7y+42

\newline

1

\newline

(A) No solutions

\newline

(B) Exactly one solution

\newline

(C) Infinitely many solutions

Posted 10 months ago

Question

How many solutions does the following equation have?

\newline

-9(x+6)=-9x+108

\newline

1

\newline

(A) No solutions

\newline

(B) Exactly one solution

\newline

(C) Infinitely many solutions

Posted 10 months ago

Question

How many solutions does the following equation have?

\newline

-6(x+7)=-4x-2

\newline

1

\newline

(A) No solutions

\newline

(B) Exactly one solution

\newline

(C) Infinitely many solutions

Posted 10 months ago

Question

How many solutions does the following equation have?

\newline

-4x-7+10x=-7+6x

\newline

1

\newline

(A) No solutions

\newline

(B) Exactly one solution

\newline

(C) Infinitely many solutions

Posted 10 months ago

Question

How many solutions does the following equation have?

\newline

-17(y-2)=-17y+64

\newline

1

\newline

(A) No solutions

\newline

(B) Exactly one solution

\newline

(C) Infinitely many solutions

Posted 10 months ago

Question

How many solutions does the following equation have?

\newline

9z-6+7z=16z-6

\newline

1

\newline

(A) No solutions

\newline

(B) Exactly one solution

\newline

(C) Infinitely many solutions

Posted 10 months ago

Related topics

Algebra - Order of Operations Algebra - Distributive Property `X` and `Y` Axes Geometry - Scalene Triangle Common Multiple Geometry - Quadrant