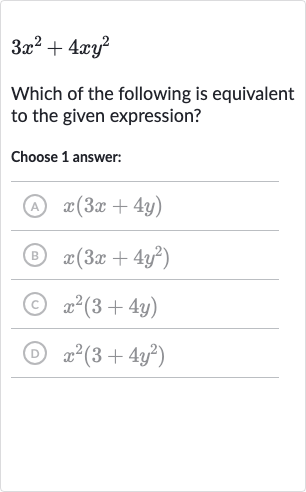
3x^(2)+4xy^(2) Which of the following is equivalent to the given expression? Choose 1 answer: (A) x(3x+4y) (B) x(3x+4y^(2)) (C) x^(2)(3+4y) (D) x^(2)(3+4y^(2))

Question

3x^(2)+4xy^(2) Which of the following is equivalent to the given expression? Choose 1 answer: (A)  x(3x+4y) (B)  x(3x+4y^(2)) (C)  x^(2)(3+4y) (D)  x^(2)(3+4y^(2))

Bytelearn · Accepted Answer

Factor Expression: We need to factor the expression 3x^(2)+4xy^(2) to see if it matches any of the given options.Identify Common Factors: First, we look for common factors in both terms. The term 3x^(2) has a factor of x, and the term 4xy^(2) also has a factor of x.Factor Out Common Factor: We factor out the common x from both terms: x(3x) + x(4y^(2)) = x(3x + 4y^(2)).Compare with Options: Now we compare the factored expression x(3x + 4y^(2)) with the given options: (A) x(3x+4y) - This is not equivalent because the y term is not squared. (B) x(3x+4y^(2)) - This is equivalent to our factored expression. (C) x^(2)(3+4y) - This is not equivalent because the x term is squared in the second factor. (D) x^(2)(3+4y^(2)) - This is not equivalent because the x term is squared in the second factor.Correct Answer: The correct answer is (B) x(3x+4y^(2)), which is equivalent to the given expression 3x^(2)+4xy^(2).

$3x^{2}+4xy^{2}$ $\newline$ Which of the following is equivalent to the given expression? $\newline$ Choose $1$ answer: $\newline$ (A) $x(3x+4y)$ $\newline$ (B) $x(3x+4y^{2})$ $\newline$ (C) $x^{2}(3+4y)$ $\newline$ (D) $x^{2}(3+4y^{2})$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

3x2+4xy23x^{2}+4xy^{2}3x2+4xy2\newlineWhich of the following is equivalent to the given expression?\newlineChoose 111 answer:\newline(A) x(3x+4y)x(3x+4y)x(3x+4y)\newline(B) x(3x+4y2)x(3x+4y^{2})x(3x+4y2)\newline(C) x2(3+4y)x^{2}(3+4y)x2(3+4y)\newline(D) x2(3+4y2)x^{2}(3+4y^{2})x2(3+4y2)

$3x^{2}+4xy^{2}$ $\newline$ Which of the following is equivalent to the given expression? $\newline$ Choose $1$ answer: $\newline$ (A) $x(3x+4y)$ $\newline$ (B) $x(3x+4y^{2})$ $\newline$ (C) $x^{2}(3+4y)$ $\newline$ (D) $x^{2}(3+4y^{2})$