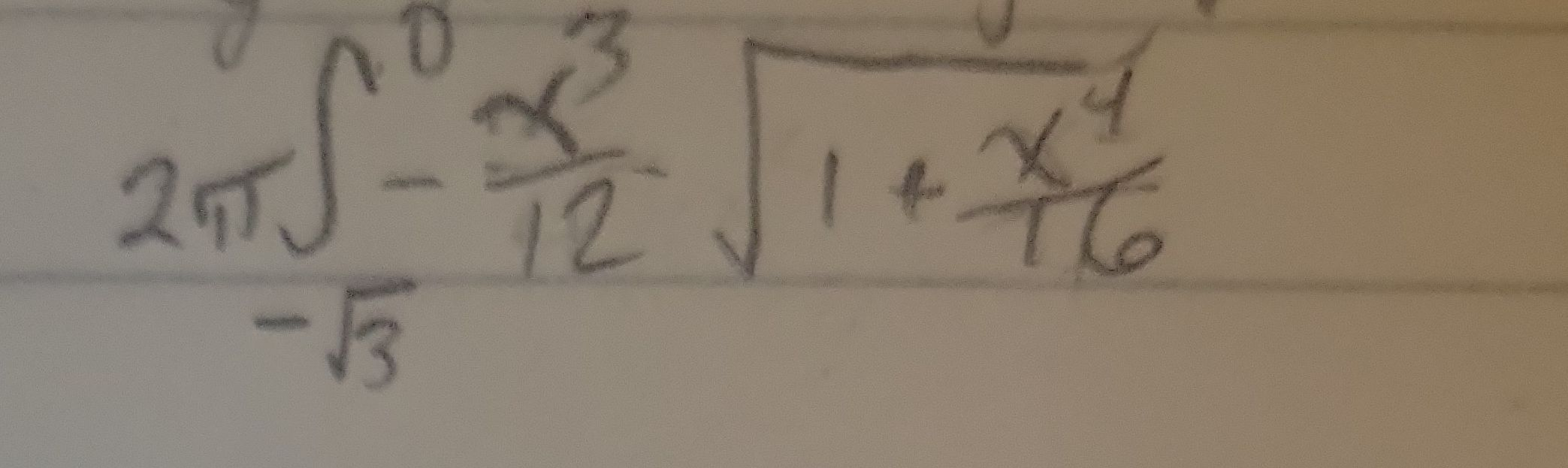2piint_(-sqrt3)^(0)-(x^(3))/(12)sqrt(1+(x^(4))/(16))

Question

Bytelearn · Accepted Answer

Simplify integrand: We are given the integral $2\pi \int_{-\sqrt{3}}^{0} -\frac{x^{3}}{12}\sqrt{1+\frac{x^{4}}{16}} \, dx$. The first step is to simplify the integrand if possible.Rewrite integral: The integrand is $-\frac{x^{3}}{12}\sqrt{1+\frac{x^{4}}{16}}$. We can simplify the square root by factoring out $x^{4}$ from the expression inside the square root to get $\sqrt{1+\frac{x^{4}}{16}} = \sqrt{\frac{16+x^{4}}{16}} = \frac{\sqrt{16+x^{4}}}{4}$.Combine constants: Now, we rewrite the integral with the simplified integrand: $2\pi \int_{-\sqrt{3}}^{0} -\frac{x^{3}}{12} \cdot \frac{\sqrt{16+x^{4}}}{4} \, dx$.Use substitution: We can simplify the integral further by combining the constants: $2\pi \int_{-\sqrt{3}}^{0} -\frac{x^{3}\sqrt{16+x^{4}}}{48} \, dx$.Adjust differential: Next, we need to evaluate the integral. This integral does not have an elementary antiderivative, so we need to use a substitution. Let $u = 16 + x^{4}$, then $du = 4x^{3} \, dx$.Express in terms of du: We need to adjust the differential $du$ to match the integrand. We have $du = 4x^{3} \, dx$, but our integrand has $-\frac{x^{3}}{48}$. To match the integrand, we divide both sides of the equation by -12: $du = -\frac{1}{12} \cdot 4x^{3} \, dx$, which gives us $du = -\frac{1}{3}x^{3} \, dx$.Simplify integral: Now we can express $x^{3} \, dx$ in terms of $du$: $x^{3} \, dx = -3du$. Substituting this into the integral, we get $2\pi \int -\frac{(-3du)\sqrt{u}}{48}$.Pull out constant: Simplify the integral: $2\pi \int \frac{3\sqrt{u}}{48} \, du$.Antiderivative of sqrt(u): We can pull out the constant: $2\pi \cdot \frac{3}{48} \int \sqrt{u} \, du$.Substitute back for u: Simplify the constant: $2\pi \cdot \frac{1}{16} \int \sqrt{u} \, du$.Evaluate at bounds: The antiderivative of $\sqrt{u}$ is $\frac{2}{3}u^{3/2}$. So, we have $2\pi \cdot \frac{1}{16} \cdot \frac{2}{3}u^{3/2}$.Calculate values: Now we need to substitute back for $u$. Since $u = 16 + x^{4}$, we have $2\pi \cdot \frac{1}{16} \cdot \frac{2}{3}(16 + x^{4})^{3/2}$.Substitute values: We need to evaluate this expression from $x = -\sqrt{3}$ to $x = 0$. When $x = 0$, $u = 16$, and when $x = -\sqrt{3}$, $u = 16 + (-\sqrt{3})^{4} = 16 + 9 = 25$.Calculate difference: Evaluating the antiderivative at the bounds gives us $2\pi \cdot \frac{1}{16} \cdot \frac{2}{3}(25^{3/2} - 16^{3/2})$.Multiply everything: Calculate the values: $25^{3/2} = 125$ and $16^{3/2} = 64$.Simplify expression: Substitute these values into the expression: $2\pi \cdot \frac{1}{16} \cdot \frac{2}{3}(125 - 64)$.Final answer: Calculate the difference: $125 - 64 = 61$.Now, multiply everything together: $2\pi \cdot \frac{1}{16} \cdot \frac{2}{3} \cdot 61$.Simplify the expression: $2\pi \cdot \frac{1}{24} \cdot 61$.Finally, multiply to get the final answer: $2\pi \cdot \frac{61}{24}$.

$2 \pi \int_{-\sqrt{3}}^{0}-\frac{x^{3}}{12} \sqrt{1+\frac{x^{4}}{16}}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

2π∫−30−x3121+x416 2 \pi \int_{-\sqrt{3}}^{0}-\frac{x^{3}}{12} \sqrt{1+\frac{x^{4}}{16}} 2π∫−3​0​−12x3​1+16x4​​

$2 \pi \int_{-\sqrt{3}}^{0}-\frac{x^{3}}{12} \sqrt{1+\frac{x^{4}}{16}}$