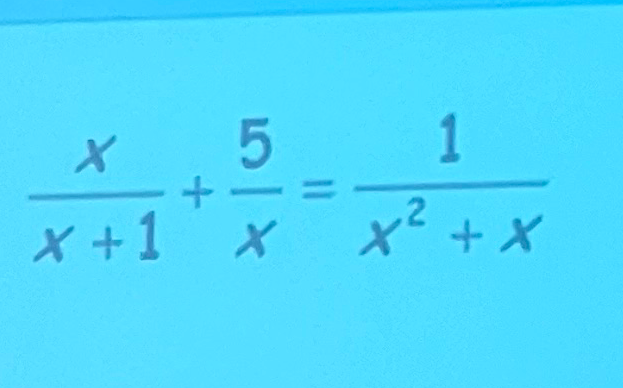(x)/(x+1)+(5)/(x)=(1)/(x^(2)+x)

Question

Bytelearn · Accepted Answer

Write Expression: First, let's write down the expression we need to simplify: (x)/(x+1) + (5)/(x) - (1)/(x^2+x)Factor Denominators: We notice that the denominators can be factored or have common factors. The denominator x^2 + x can be factored as x(x + 1).Rewrite with Factored Denominator: Now, let's rewrite the expression with the factored denominator for the third term: (x)/(x+1) + (5)/(x) - (1)/(x(x+1))Find Common Denominator: To combine these fractions, we need a common denominator. The least common denominator (LCD) for the terms is x(x+1).Rewrite with Common Denominator: We will rewrite each fraction with the common denominator x(x+1): (x)/(x+1) * (x/x) + (5)/(x) * ((x+1)/(x+1)) - (1)/(x(x+1))Multiply Numerators: Now, multiply the numerators by the appropriate factors to get the common denominator: (x^2)/(x(x+1)) + (5(x+1))/(x(x+1)) - (1)/(x(x+1))Combine Numerators: Combine the numerators over the common denominator: (x^2 + 5x + 5 - 1)/(x(x+1))Simplify Numerator: Simplify the numerator by combining like terms: (x^2 + 5x + 4)/(x(x+1))Final Simplified Expression: Now we have the expression in a single fraction. This is the simplified form of the original expression.

$\frac{x}{x+1}+\frac{5}{x}=\frac{1}{x^{2}+x}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

xx+1+5x=1x2+x \frac{x}{x+1}+\frac{5}{x}=\frac{1}{x^{2}+x} x+1x​+x5​=x2+x1​

$\frac{x}{x+1}+\frac{5}{x}=\frac{1}{x^{2}+x}$