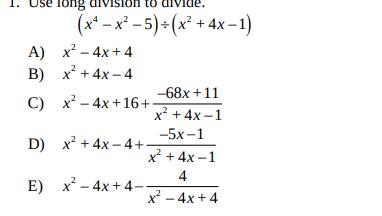AI tutor
Full solution
Q. A) B) C) D) E)
- Divide Leading Terms: To solve this problem, we will perform polynomial long division. We will divide the polynomial in the numerator, , by the polynomial in the denominator, .
- Subtract and Simplify: First, we divide the leading term of the numerator, , by the leading term of the denominator, , to get . This will be the first term of our quotient.
- Divide New Leading Term: Next, we multiply the entire denominator, , by the term we just found, , and subtract this from the numerator.
- Subtract and Simplify: Simplify the subtraction by combining like terms.
- Divide New Leading Term: Now, we divide the new leading term of the remainder, , by the leading term of the denominator, , to get . This will be the next term of our quotient.
- Subtract and Simplify: We multiply the entire denominator, , by the term we just found, , and subtract this from the current remainder.
- Final Remainder: Simplify the subtraction by combining like terms.
- Final Remainder: Simplify the subtraction by combining like terms. Now, we divide the new leading term of the remainder, , by the leading term of the denominator, , to get . This will be the next term of our quotient.
- Final Remainder: Simplify the subtraction by combining like terms. Now, we divide the new leading term of the remainder, , by the leading term of the denominator, , to get . This will be the next term of our quotient.We multiply the entire denominator, , by the term we just found, , and subtract this from the current remainder.
- Final Remainder: Simplify the subtraction by combining like terms. Now, we divide the new leading term of the remainder, , by the leading term of the denominator, , to get . This will be the next term of our quotient.We multiply the entire denominator, , by the term we just found, , and subtract this from the current remainder.Simplify the subtraction by combining like terms.
- Final Remainder: Simplify the subtraction by combining like terms. Now, we divide the new leading term of the remainder, , by the leading term of the denominator, , to get . This will be the next term of our quotient.We multiply the entire denominator, , by the term we just found, , and subtract this from the current remainder.Simplify the subtraction by combining like terms.The remainder is now , which cannot be divided by the denominator since its degree is lower than the degree of the denominator. Therefore, the remainder will be written as a fraction over the original denominator.
- Final Remainder: Simplify the subtraction by combining like terms.Now, we divide the new leading term of the remainder, , by the leading term of the denominator, , to get . This will be the next term of our quotient.We multiply the entire denominator, , by the term we just found, , and subtract this from the current remainder.Simplify the subtraction by combining like terms.The remainder is now , which cannot be divided by the denominator since its degree is lower than the degree of the denominator. Therefore, the remainder will be written as a fraction over the original denominator.Combine all the terms we found for the quotient and write the remainder as a fraction over the denominator to get the final answer.