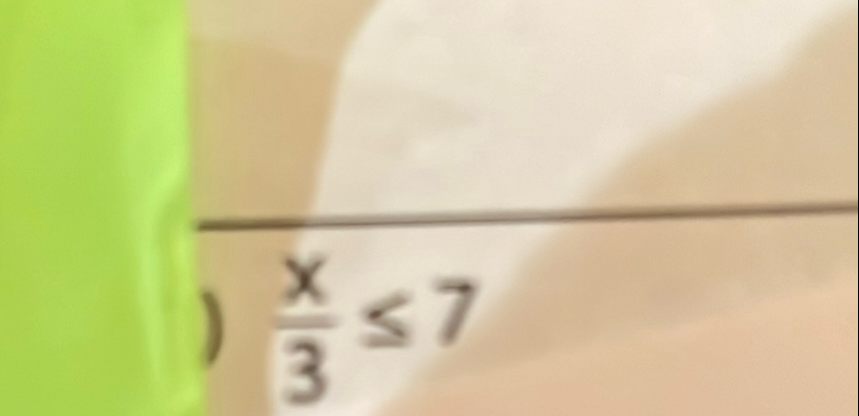Resourcesdown chevron
Testimonials
Plans
Sign in
Sign up
Resourcesright arrow
Testimonials
Plans
Bytelearn - cat image with glassesAI tutor

Welcome to Bytelearn!

Let’s check out your problem:

(x)/(3) <= 7

x3≤7 \frac{x}{3} \leq 7

View step-by-step helpView step-by-step help
Homeright chevron icon
Math Problemsright chevron icon
Grade 7right chevron icon
Powers with decimal and fractional basesright chevron icon

Full solution

Q. x3≤7 \frac{x}{3} \leq 7
  1. Multiply by 33: To solve the inequality (x3)≤7(\frac{x}{3}) \leq 7, we need to isolate xx. We can do this by multiplying both sides of the inequality by 33, which is the denominator of the fraction on the left side.\newlineCalculation: 3×(x3)≤3×73 \times (\frac{x}{3}) \leq 3 \times 7
  2. Cancel out 33: After multiplying both sides by 33, the 33 on the left side cancels out with the denominator of the fraction, leaving us with xx on the left side.\newlineCalculation: x≤3×7x \leq 3 \times 7
  3. Multiply by 77: Now we multiply 33 by 77 to find the value that xx must be less than or equal to.\newlineCalculation: x≤21x \leq 21
  4. Final Solution: The inequality x≤21x \leq 21 means that xx can be any real number less than or equal to 2121. This is the solution set for the inequality.

More problems from Powers with decimal and fractional bases

Question
Write the expression using an exponent.\newline2×22 \times 2\newline______
Get tutor helpright-arrow

Posted 2 months ago

Question
Evaluate the expression. 4−42 4 - 4^2 ____
Get tutor helpright-arrow

Posted 2 months ago

Question
x2=4x^2 = 4
Get tutor helpright-arrow

Posted 1 month ago

Question
x2=9x^2 = 9
Get tutor helpright-arrow

Posted 3 months ago

Question
Solve for x. \newlinex2=0x^2 = 0 \newlineWrite your answer in simplified, rationalized form. \newlinex=x = _____ or x=x = _____
Get tutor helpright-arrow

Posted 3 months ago

Question
Solve for xx. \newline8=2x8 = 2^x \newline x=x = _____
Get tutor helpright-arrow

Posted 3 months ago

Question
Solve for xx. \newline6=7x6 = 7^x \newline x=x = _____
Get tutor helpright-arrow

Posted 3 months ago

Question
Select the equivalent expression.\newline((8−5)/(2−2))−4=?((8^{-5})/(2^{-2}))^{-4}=?\newlineChoose 11 answer:\newline(A) \newline(820)/(28)(8^{20})/(2^{8})\newline(B) \newline(26)/(89)(2^{6})/(8^{9})\newline(C) \newline(1)/(8⋅22)(1)/(8\cdot 2^{2})
Get tutor helpright-arrow

Posted 4 days ago

Question
Select the equivalent expression.\newline(b745)−3= ?\left(\frac{b^{7}}{4^{5}}\right)^{-3}=\,?\newlineChoose 11 answer:\newline(A) b21415\frac{b^{21}}{4^{15}}\newline(B) 415b21\frac{4^{15}}{b^{21}}\newline(C) b−21⋅4−15b^{-21}\cdot 4^{-15}
Get tutor helpright-arrow

Posted 1 month ago

Question
Select the equivalent expression.\newline(33⋅66)−3=(3^{3}\cdot6^{6})^{-3}=?\newlineChoose 11 answer:\newline(A) 139⋅618\frac{1}{3^{9}\cdot6^{18}}\newline(B) 61839\frac{6^{18}}{3^{9}}\newline(C) 39618\frac{3^{9}}{6^{18}}
Get tutor helpright-arrow

Posted 1 month ago

View all (52)