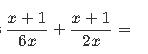(x+1)/(6x)+(x+1)/(2x)=

Question

Bytelearn · Accepted Answer

Identify Terms: Identify the terms to be added. We have two fractions: (x+1)/(6x) and (x+1)/(2x). We need to find a common denominator to add them together.Find LCD: Find the least common denominator (LCD) of the two fractions. The denominators are 6x and 2x. The LCD of 6x and 2x is 6x because 6x is the smallest number that both 2x and 6x can divide into without a remainder.Rewrite Fractions: Rewrite each fraction with the LCD as the denominator. The first fraction (x+1)/(6x) already has the LCD as its denominator, so it remains unchanged. The second fraction (x+1)/(2x) needs to be rewritten. To make 2x into 6x, we multiply the numerator and the denominator by 3. So, (x+1)/(2x) becomes 3(x+1)/(6x).Add Fractions: Add the two fractions with the common denominator. Now we have (x+1)/(6x) + 3(x+1)/(6x). Since the denominators are the same, we can add the numerators directly. (x+1) + 3(x+1) = (x+1) + (3x+3)Simplify Numerator: Simplify the combined numerator. (x+1) + (3x+3) = x + 1 + 3x + 3 Combine like terms: x + 3x = 4x and 1 + 3 = 4 So, the combined numerator is 4x + 4.Write Over Common Denominator: Write the simplified numerator over the common denominator. The simplified expression is (4x + 4)/(6x).Factor Out Common Factors: Simplify the fraction by factoring out common factors if possible. Both the numerator and the denominator have a common factor of 2. Divide both the numerator and the denominator by 2 to simplify the fraction. (4x + 4)/(6x) = 2(2x + 2)/(2*3x) = (2x + 2)/(3x)

$\frac{x+1}{6 x}+\frac{x+1}{2 x}=$

Full solution

More problems from Powers with negative bases

Related topics

x+16x+x+12x= \frac{x+1}{6 x}+\frac{x+1}{2 x}= 6xx+1​+2xx+1​=

$\frac{x+1}{6 x}+\frac{x+1}{2 x}=$