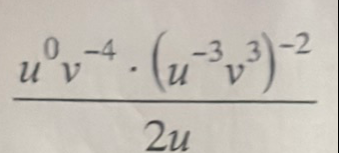AI tutor
Full solution
Q.
- Simplify and Apply Exponent Rule: First, simplify the expression inside the parentheses and apply the exponent rule to the term .
- Combine Like Terms: Next, combine the like terms by adding the exponents of and .
- Divide by u: Now, divide the simplified expression by u.
- Simplify by Subtracting Exponents: Simplify the expression by subtracting the exponents of .
- Write Negative Exponent as Reciprocal: Finally, write the negative exponent as a reciprocal to express the answer without negative exponents.