AI tutor
Full solution
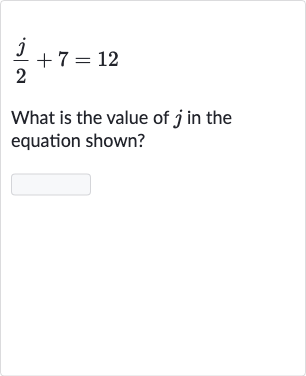
Q. What is the value of in the equation shown?
- Subtract : We are given the equation . To solve for , we first need to isolate the term containing on one side of the equation. We can do this by subtracting from both sides of the equation to get rid of the constant term on the left side.Calculation:
- Simplify Equation: After subtracting from both sides, we simplify the equation to find the term with alone on one side.Calculation:
- Multiply by : Now, to solve for , we need to get rid of the fraction by multiplying both sides of the equation by , which is the denominator of the fraction.Calculation:
- Cancel Denominator: Multiplying both sides by cancels out the denominator on the left side, leaving us with on the left side and the product of and on the right side.Calculation:
More problems from Solve linear equations: mixed review
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help