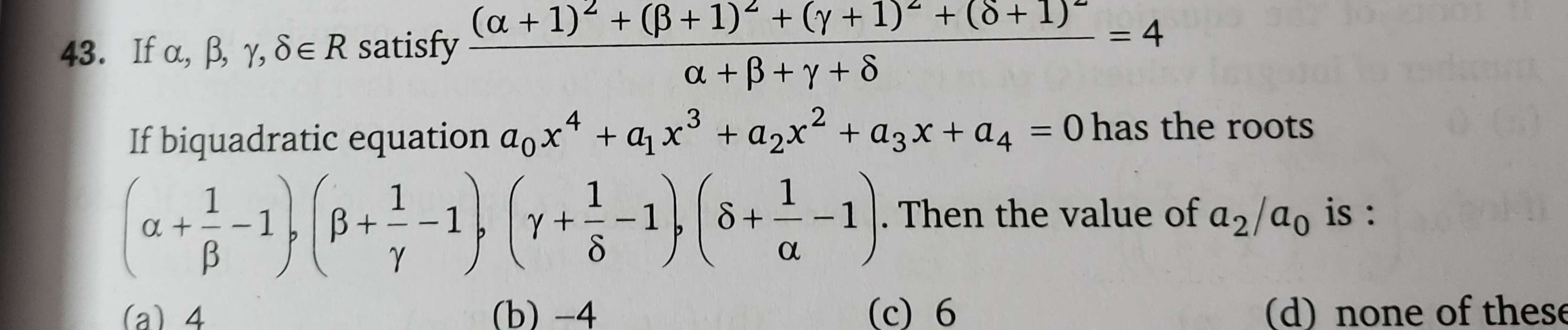: If alpha,beta,gamma,delta in R satisfy ((alpha+1)^(2)+(beta+1)^(2)+(gamma+1)^(2)+(delta+1)^(2))/(alpha+beta+gamma+delta)=4 If biquadratic equation a_(0)x^(4)+a_(1)x^(3)+a_(2)x^(2)+a_(3)x+a_(4)=0 has the roots (alpha+(1)/(beta)-1),(beta+(1)/(gamma)-1),(gamma+(1)/(delta)-1),(delta+(1)/(alpha)-1). Then the value of a_(2)//a_(0) is : (a) 4 (b) -4 (c) 6 (d) none of these

Question

: If  alpha,beta,gamma,delta in R satisfy  ((alpha+1)^(2)+(beta+1)^(2)+(gamma+1)^(2)+(delta+1)^(2))/(alpha+beta+gamma+delta)=4 If biquadratic equation  a_(0)x^(4)+a_(1)x^(3)+a_(2)x^(2)+a_(3)x+a_(4)=0 has the roots  (alpha+(1)/(beta)-1),(beta+(1)/(gamma)-1),(gamma+(1)/(delta)-1),(delta+(1)/(alpha)-1). Then the value of  a_(2)//a_(0) is : (a) 4 (b) -4 (c) 6 (d) none of these

Bytelearn · Accepted Answer

Expand and Simplify: Given the equation: ((alpha+1)^(2)+(beta+1)^(2)+(gamma+1)^(2)+(delta+1)^(2))/(alpha+beta+gamma+delta)=4 We can simplify this equation by expanding the squares and then dividing by the sum of alpha, beta, gamma, and delta.Divide by Sum: Expanding the numerator, we get: (alpha^2 + 2alpha + 1) + (beta^2 + 2beta + 1) + (gamma^2 + 2gamma + 1) + (delta^2 + 2delta + 1) This simplifies to: (alpha^2 + beta^2 + gamma^2 + delta^2) + 2(alpha + beta + gamma + delta) + 4Set up Equation: Now, we divide by the sum of alpha, beta, gamma, and delta: ((alpha^2 + beta^2 + gamma^2 + delta^2) + 2(alpha + beta + gamma + delta) + 4) / (alpha + beta + gamma + delta) This simplifies to: (alpha + beta + gamma + delta) + 2 + 4/(alpha + beta + gamma + delta) Given that the whole expression equals 4, we can set up the equation: (alpha + beta + gamma + delta) + 2 + 4/(alpha + beta + gamma + delta) = 4Solve for S: We can now solve for (alpha + beta + gamma + delta): (alpha + beta + gamma + delta) + 4/(alpha + beta + gamma + delta) = 2 Let's denote S = alpha + beta + gamma + delta. Then we have: S + 4/S = 2 Multiplying both sides by S to clear the fraction, we get: S^2 + 4 = 2SQuadratic Equation: Rearranging the terms, we get a quadratic equation in S: S^2 - 2S + 4 = 0 This equation does not have real roots, which means there is a math error in our previous steps. We need to re-evaluate our approach to solving for S.

Full solution

More problems from Find derivatives of using multiple formulae

Related topics