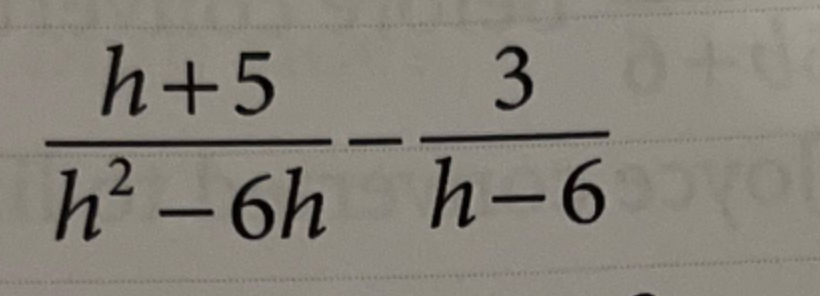AI tutor
Full solution
Q. Solve for :
- Find Common Denominator: Combine the two fractions into one by finding a common denominator.The common denominator is , which can be factored into .
- Rewrite with Common Denominator: Rewrite each fraction with the common denominator. becomes .
- Subtract Fractions: Subtract the second fraction from the first. .
- Simplify Numerator: Simplify the numerator. .
- Check for Simplification: Check for any possible simplification or factoring.The numerator and denominator have no common factors, so this is the final simplified form.