AI tutor
Full solution
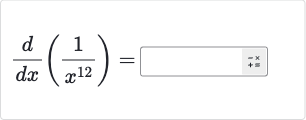
Q.
- Rewrite function: We are asked to find the derivative of the function with respect to . To do this, we will use the power rule for differentiation, which states that the derivative of with respect to is . In this case, we can rewrite the function as to apply the power rule.
- Apply power rule: Applying the power rule, we differentiate with respect to . According to the power rule, the derivative of is . Therefore, the derivative of is or .
- Rewrite derivative: We can rewrite the derivative in a more conventional form by moving the negative exponent back to the denominator. So, the derivative becomes .
- Final answer: We have found the derivative of the function with respect to , which is . This is the final answer.
More problems from Multiplication with rational exponents
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help
QuestionGet tutor help