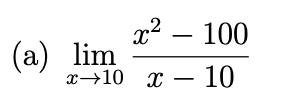Find the limit as x approaches 10 of lim_(x rarr10)(x^(2)-100)/(x-10)

Question

Find the limit as  x approaches 10 of  lim_(x rarr10)(x^(2)-100)/(x-10)

Bytelearn · Accepted Answer

Substitution Check: First, let's try to directly substitute the value x = 10 into the function to see if it results in an indeterminate form. Substitute x = 10 into (x^2 - 100)/(x - 10): (10^2 - 100)/(10 - 10) = (100 - 100)/(10 - 10) = 0/0. This is an indeterminate form, so we cannot directly evaluate the limit by substitution.Simplify Expression: Since we have an indeterminate form of 0/0, we should try to simplify the expression to eliminate the common factor in the numerator and the denominator. Factor the numerator: x^2 - 100 = (x + 10)(x - 10). Now the function becomes ((x + 10)(x - 10))/(x - 10).Cancel Common Factor: Next, we cancel out the common factor (x - 10) in the numerator and the denominator, as long as x is not equal to 10 (which it isn't, since we are taking a limit as x approaches 10, not evaluating at x = 10). The function simplifies to: (x + 10) when x ≠ 10.Final Substitution: Now that we have simplified the function, we can directly substitute x = 10 to find the limit. Substitute x = 10 into (x + 10): 10 + 10 = 20.Limit Calculation: The limit as x approaches 10 of the function (x^2 - 100)/(x - 10) is 20.

Find the limit as $𝑥$ approaches 10 of $\lim_{x \to 10}\frac{x^{2}-100}{x-10}$

Full solution

More problems from Find derivatives of using multiple formulae

Related topics

Find the limit as 𝑥𝑥x approaches 10 of lim⁡x→10x2−100x−10\lim_{x \to 10}\frac{x^{2}-100}{x-10}limx→10​x−10x2−100​

Find the limit as $𝑥$ approaches 10 of $\lim_{x \to 10}\frac{x^{2}-100}{x-10}$